题目内容
2.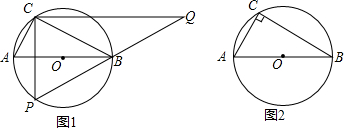 如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.
如图,AB为⊙O的直径,点C为圆上一定点,AC=6,BC=8,P为⊙O上一动点,过C作CQ⊥CP,交PB延长线于Q.(1)若AB⊥CP,如图1,求CQ的长;
(2)当P点运动到何处时,△PCQ的内心在线段CB上,请利用图2说明理由并求出CP的长.
分析 (1)如图1中,假设AB与PC交于点H,由△ACH∽△ABC,得$\frac{AC}{AB}$=$\frac{AH}{AC}$,求出AH、BH,再证明BH是△PCQ中位线即可解决问题.
(2)如图2中,当点P是$\widehat{AB}$中点时,BC平分∠PCQ,此时△PCQ的内心在线段BC上.作BM⊥PC于M.,易证△CMB是等腰直角三角形,求出CM、BM,再由
△ABC∽△PBM,得$\frac{BC}{BM}$=$\frac{AC}{MP}$,求出PM即可解决问题.
解答 解:(1)如图1中,假设AB与PC交于点H,
∵AB是直径,PC⊥AB,
∴∠ACB=∠AHC=90°,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴$\widehat{AC}$=$\widehat{AP}$,PH=CH,
∴∠ACH=∠ABC,
∴△ACH∽△ABC,
∴$\frac{AC}{AB}$=$\frac{AH}{AC}$,
∴AH=$\frac{18}{5}$,BH=$\frac{32}{5}$,
∵PC⊥CQ,
∴BH∥QC,
∴PB=BQ,
∴CQ=2BH=$\frac{64}{5}$.
(2)如图2中,当点P是$\widehat{AB}$中点时,BC平分∠PCQ,此时△PCQ的内心在线段BC上.作BM⊥PC于M.
∵在RT△BCM中,∠PCB=45°,BC=8,
∴CM=BM=4$\sqrt{2}$,
∵∠ABP=∠ACP=∠MBC=45°,
∴∠PBM=∠ABC,∵∠ACB=∠PMB=90°,
∴△ABC∽△PBM,
∴$\frac{BC}{BM}$=$\frac{AC}{MP}$,
∴$\frac{8}{4\sqrt{2}}$=$\frac{6}{PM}$,
∴PM=3$\sqrt{2}$,
∴PC=CM+PM=7$\sqrt{2}$.
点评 本题考查三角形内心外心,相似三角形的判定和性质、圆的有关性质、勾股定理等知识,解题的关键是正确寻找相似三角形,学会添加常用辅助线,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案| A. | 小王参加本次数学考试,成绩是500分 | |
| B. | 某射击运动员射靶一次,正中靶心 | |
| C. | 打开电视机,CCTV第一套节目正在播放新闻 | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
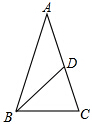 如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )
如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | x为任意实数 | B. | x≥3 | C. | x>3 | D. | x≤3 |
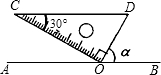 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
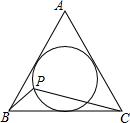 点P是边长8$\sqrt{3}$的正三角形ABC的内切圆的一个动点,求BP+$\frac{1}{2}$PC的最小值2$\sqrt{21}$.
点P是边长8$\sqrt{3}$的正三角形ABC的内切圆的一个动点,求BP+$\frac{1}{2}$PC的最小值2$\sqrt{21}$.