题目内容
2.已知a>-2,若当1≤x≤2时,函数y=$\frac{a}{x}$(a≠0)的最大值与最小值之差是1,求a的值.分析 此题要把a的取值范围分成两种情况:(1)当-2<a<0时,(2)当a>0时,再分别根据反比例函数的性质去x=1,x=2时列出方程求解.
解答 解法1:(1)当-2<a<0时,
在1≤x≤2范围内y随x的增大而增大,
∴$\frac{a}{2}$-a=1.
∴a=-2
不合题意,舍去.
(2)当a>0时,
在1≤x≤2范围内y随x的增大而减小,
∴a-$\frac{a}{2}$=1.
∴a=2.
综上所述a=2.
解法2:(1)当a<0时,
在1≤x≤2范围内y随x的增大而增大,
∴$\frac{a}{2}$-a=1.
∴a=-2.
又∵-2<a<0
∴a=-2不合题意,舍去.
(2)当a>0时,
在1≤x≤2范围内y随x的增大而减小,
∴a-$\frac{a}{2}$=1.
∴a=2.
∴b=1.而a2-ab+2=4>0,符合题意,
∴a=2.
综上所述,a=2.
点评 此题主要考查了反比例函数的性质,关键是掌握反比例函数的性质(1)反比例函数y=$\frac{k}{x}$(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.注意:反比例函数的图象与坐标轴没有交点.

练习册系列答案
相关题目
12.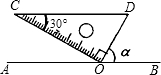 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
13.已知一次函数y=-3x+4,则下列说法中不正确的是( )
| A. | 该函数的图象经过点(1,1) | |
| B. | 该函数的图象不经过第三象限 | |
| C. | y的值随x的值的增大而减小 | |
| D. | 该函数的图象与x轴的交点坐标为(-$\frac{4}{3}$,0) |
10.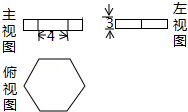 如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )
如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )
 如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )
如图是某几何体的三视图,其俯视图为正六边形,则该几何体的体积是( )| A. | 24$\sqrt{3}$ | B. | 36$\sqrt{3}$ | C. | 72$\sqrt{3}$ | D. | 144$\sqrt{3}$ |
7.一次函数y=x+1的图象是( )
| A. | 线段 | B. | 抛物线 | C. | 直线 | D. | 双曲线 |
 如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=$\frac{1}{3}$AB,AF=$\frac{1}{4}$AD,连结EF交对角线AC于G,则$\frac{AG}{AC}$=$\frac{1}{7}$.
如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=$\frac{1}{3}$AB,AF=$\frac{1}{4}$AD,连结EF交对角线AC于G,则$\frac{AG}{AC}$=$\frac{1}{7}$.