题目内容
3.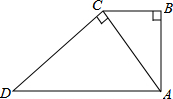 如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则
如图,Rt△ABC和Rt△DCA中,∠B=∠ACD=90°,AD∥BC,AB=2,DC=3,则△ABC与△DCA的面积比为( )
| A. | 2:3 | B. | 2:5 | C. | 4:9 | D. | $\sqrt{2}$:$\sqrt{3}$ |
分析 由AD∥BC,得出∠ACB=∠DAC,证得△ABC∽△DCA,再由面积的比等于相似比的平方,即可得到问题答案.
解答 解:∵AD∥BC,
∴∠ACB=∠DAC
又∵∠B=∠ACD=90°,
∴△CBA∽△ACD,
∴$\frac{AB}{DC}=\frac{BC}{AC}=\frac{AC}{AD}$,
∵AB=2,DC=3,
∴$\frac{AB}{DC}=\frac{2}{3}$,
∴$\frac{{S}_{△ABC}}{{S}_{△DCA}}=(\frac{AB}{DC})^{2}$=$\frac{4}{9}$,
故选C.
点评 本题考查了相似三角形的判定与性质以及平行线的性质,通过证明三角形相似得出面积比等于相似比的平方是解决问题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
11.下列事件为必然事件的是( )
| A. | 小王参加本次数学考试,成绩是500分 | |
| B. | 某射击运动员射靶一次,正中靶心 | |
| C. | 打开电视机,CCTV第一套节目正在播放新闻 | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
14.若$\sqrt{{x^2}-6x+9}$=3-x,则x的取值范围是( )
| A. | x为任意实数 | B. | x≥3 | C. | x>3 | D. | x≤3 |
18.下列说法中,正确的是( )
| A. | 在同一平面内,不相交的两条直线必平行 | |
| B. | 过任意一点可作一条已知直线的平行线 | |
| C. | 两条直线被第三条直线所截,所得到同位角相等 | |
| D. | 两条直线的交点叫做垂足 |
8.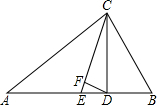 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )| A. | 20° | B. | 60° | C. | 70° | D. | 80° |
15.若a<2$\sqrt{2}$<b,其中a、b为两个连续的整数,则ab的值为( )
| A. | 2 | B. | 5 | C. | 6 | D. | 12 |
12.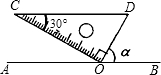 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
13.已知一次函数y=-3x+4,则下列说法中不正确的是( )
| A. | 该函数的图象经过点(1,1) | |
| B. | 该函数的图象不经过第三象限 | |
| C. | y的值随x的值的增大而减小 | |
| D. | 该函数的图象与x轴的交点坐标为(-$\frac{4}{3}$,0) |
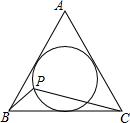 点P是边长8$\sqrt{3}$的正三角形ABC的内切圆的一个动点,求BP+$\frac{1}{2}$PC的最小值2$\sqrt{21}$.
点P是边长8$\sqrt{3}$的正三角形ABC的内切圆的一个动点,求BP+$\frac{1}{2}$PC的最小值2$\sqrt{21}$.