题目内容
17. 已知抛物线y=ax2+bx+c的部分图象如图所示,若y<0,则x的取值范围是-1<x<3.
已知抛物线y=ax2+bx+c的部分图象如图所示,若y<0,则x的取值范围是-1<x<3.
分析 首先求出点(-1,0)关于对称轴x=1的对称点,进而结合图象可得当y<0时x的取值范围.
解答 解:根据图象可知,抛物线的对称轴为x=1,
抛物线与x轴的一个交点为(-1,0),
则(-1,0)关于x=1对称的点为(3,0),
即抛物线与x轴另一个交点为(3,0),
当-1<x<3时,y<0,
故答案为:-1<x<3.
点评 本题主要考查了抛物线与x轴的交点的知识,解答本题的关键是求出抛物线与x轴的另一个交点坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.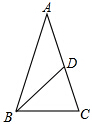 如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )
如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )
 如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )
如图,在△ABC中,AB=AC,∠A=36°,BD分别是△ABC的角平分线,则图中的等腰三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.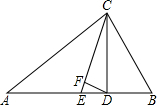 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
 如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )
如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=( )| A. | 20° | B. | 60° | C. | 70° | D. | 80° |
5.已知在Rt△ABC中,∠C=90°,AC=2,BC=3,则AB的长为( )
| A. | 4 | B. | $\sqrt{5}$ | C. | $\sqrt{13}$ | D. | 5 |
12.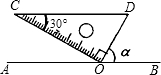 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
6. 如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
 如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图,二次函数y=ax2+bx+c图象的一部分,对称轴为x=$\frac{1}{2}$,且经过(2,0)这个点,有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )| A. | ①②③④ | B. | ③④ | C. | ①③④ | D. | ①② |
7.一次函数y=x+1的图象是( )
| A. | 线段 | B. | 抛物线 | C. | 直线 | D. | 双曲线 |
 已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形ABCD边BC的中点F,交CD于点E,四边形AFCE的面积为2,则k的值为2.
已知反比例函数y=$\frac{k}{x}$(x>0)的图象经过矩形ABCD边BC的中点F,交CD于点E,四边形AFCE的面积为2,则k的值为2.