题目内容
7. 如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )
如图,教师在小黑板上出示一道题,小华答:过点(3,0);小彬答:过点(4,3);小明答:a=1;小颖答:抛物线被x轴截得的线段长为2.你认为四人的回答中,正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据图上给出的条件是与x轴交于(1,0),叫我们加个条件使对称轴是x=2,意思就是抛物线的对称轴是x=2是题目的已知条件,这样可以求出a、b的值,然后即可判断题目给出四个人的判断是否正确.
解答 解:∵抛物线过(1,0),对称轴是x=2,
∴$\left\{\begin{array}{l}{a+b+3=0}\\{-\frac{b}{2a}=2}\end{array}\right.$,
解得a=1,b=-4,
∴y=x2-4x+3,
当x=3时,y=0,小华正确;
当x=4时,y=3,小彬也正确,小明也正确;
∵抛物线被x轴截得的线段长为2,已知过点(1,0),
∴另一点为(-1,0)或(3,0),
∴对称轴为y轴或x=2,此时答案不唯一,
∴小颖错误.
故选C.
点评 本题是开放性题目,考查了抛物线与x轴的交点、抛物线解析式的求法等知识;根据题意求出抛物线的解析式是解决问题的关键.

练习册系列答案
相关题目
18.下列说法中,正确的是( )
| A. | 在同一平面内,不相交的两条直线必平行 | |
| B. | 过任意一点可作一条已知直线的平行线 | |
| C. | 两条直线被第三条直线所截,所得到同位角相等 | |
| D. | 两条直线的交点叫做垂足 |
15.若a<2$\sqrt{2}$<b,其中a、b为两个连续的整数,则ab的值为( )
| A. | 2 | B. | 5 | C. | 6 | D. | 12 |
12.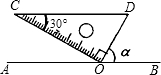 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
 如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )
如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB,则∠α的正弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
 如图,在直角体系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),C是y轴上的点.
如图,在直角体系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),C是y轴上的点. 如图,反比例函数y=$\frac{4}{x}$的图象与一次函数y=kx-3的图象在第一象限内相交于点A,且点A的横坐标为4.
如图,反比例函数y=$\frac{4}{x}$的图象与一次函数y=kx-3的图象在第一象限内相交于点A,且点A的横坐标为4. 如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=$\frac{1}{3}$AB,AF=$\frac{1}{4}$AD,连结EF交对角线AC于G,则$\frac{AG}{AC}$=$\frac{1}{7}$.
如图,在平行四边形ABCD中,点E、F分别在AB、AD上,且AE=$\frac{1}{3}$AB,AF=$\frac{1}{4}$AD,连结EF交对角线AC于G,则$\frac{AG}{AC}$=$\frac{1}{7}$.