题目内容
11.阅读材料:材料1、若一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=$-\frac{b}{a}$,x1x2=$\frac{c}{a}$.
材料2、已知实数m、n满足m2-m-1=0,n2-n-1=0,且m≠n,求$\frac{n}{m}+\frac{m}{n}$的值.
解:由题知m、n是方程x2-x-1=0的两个不相等的实数根,根据材料1得
m+n=1,mn=-1
∴$\frac{n}{m}+\frac{m}{n}=\frac{{m}^{2}+{n}^{2}}{mn}=\frac{(m+n)^{2}-2mn}{mn}$=$\frac{1+2}{-1}=-3$
根据上述材料解决下面问题;
(1)一元二次方程2x2+3x-1=0的两根为x1、x2,则x1+x2=-$\frac{3}{2}$,x1x2=-$\frac{1}{2}$.
(2)已知实数m、n满足2m2-2m-1=0,2n2-2n-1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p、q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2的值.
分析 (1)直接根据根与系数的关系求解;
(2)利用m、n满足的等式,可把m、n可看作方程2x2-2x-1=0的两实数解,则根据根与系数的关系得到m+n=1,mn=-$\frac{1}{2}$,接着把m2n+mn2分解得到mn(m+n),然后利用整体代入的方法计算;
(3)先设t=2q,代入2q2=3q+1化简得到t2=3t+2,根据p与t满足的等式可把p与t(即2q)为方程x2-3x-2=0的两实数解,则根据根与系数的关系得到p+2q=3,p•2q=-2,接着利用完全平方公式变形得到p2+4q2=(p+2q)2-2p•2q,然后利用整体代入的方法计算.
解答 解:(1)x1+x2=-$\frac{3}{2}$,x1x2=-$\frac{1}{2}$;
故答案为-$\frac{3}{2}$,-$\frac{1}{2}$;
(2)∵m、n满足2m2-2m-1=0,2n2-2n-1=0,
∴m、n可看作方程2x2-2x-1=0的两实数解,
∴m+n=1,mn=-$\frac{1}{2}$,
∴m2n+mn2=mn(m+n)=-$\frac{1}{2}$×1=-$\frac{1}{2}$;
(3)设t=2q,代入2q2=3q+1化简为t2=3t+2,
则p与t(即2q)为方程x2-3x-2=0的两实数解,
∴p+2q=3,p•2q=-2,
∴p2+4q2=(p+2q)2-2p•2q=32-2×(-2)=13.
点评 本题考查了根与系数的关系:二次项系数不为1,则常用以下关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
2.在下列运算中,正确的是( )
| A. | 4x+2y=6xy | B. | 2x3•x2=2x5 | C. | (x2)3=x5 | D. | (3xy)2÷(xy)=3xy |
19.使$\sqrt{x+1}$有意义的x的取值范围是( )
| A. | x≥-1 | B. | x<1 | C. | x>-1 | D. | x≤1 |
16.截至2014年1月初,济南户籍总人口613.4万人,其中613.4万人用科学记数法表示为( )
| A. | 6.134×102人 | B. | 613.4×104人 | C. | 6.134×105人 | D. | 6.134×106人 |
20.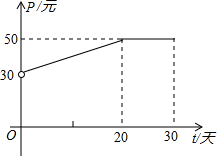 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
(1)根据图象,写出该产品每件销售价格P与时间t的函数解析式;
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量.
 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量.
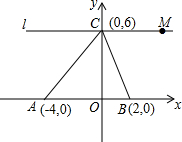 如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)
如图所示,A、B、C三点的坐标分别为:A(-4,0)、B(2,0)、C(0,6)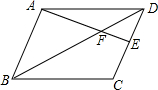 在?ABCD中,点E为CD的中点,连接BD交AE于点F,则AF:FE=2:1.
在?ABCD中,点E为CD的中点,连接BD交AE于点F,则AF:FE=2:1. 已知实数a、b在数轴上的位置如图所示,则化简$\sqrt{(a-b)^{2}}$的结果是-a+b.
已知实数a、b在数轴上的位置如图所示,则化简$\sqrt{(a-b)^{2}}$的结果是-a+b.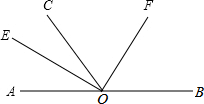 如图,AOB是一条直线,OC是一条射线,∠AOC=60°,OE、OF分别是∠AOC、∠BOC平分线.
如图,AOB是一条直线,OC是一条射线,∠AOC=60°,OE、OF分别是∠AOC、∠BOC平分线.