题目内容
1．
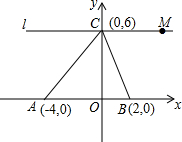如图所示，A、B、C三点的坐标分别为：A（-4，0）、B（2，0）、C（0，6）（1）求S△ABC；
（2）过C点作直线l平行于x轴，M为l上任意一点，试猜想S△CAB与S△MAB的关系？请用特值验证你的猜想；
（3）试求坐标轴上找一点P，使S△ACP=$\frac{1}{2}$S△ABC，请直接写出满足条件的P的坐标．
分析 （1）由图可知：AB=6，OC=6，即可求△ABC的面积；
（2）猜想：S△ABC=S△MAB，根据三角形的面积公式进行验证；
（3）根据S△ACP=$\frac{1}{2}$S△ABC，分别在x轴，y轴上找到点P．
解答 解：（1）由图可知：AB=6，OC=6，
∴${S}_{△ABC}=\frac{1}{2}×6×6$=18．
（2）猜想：S△ABC=S△MAB
如图1，连接MA，MB，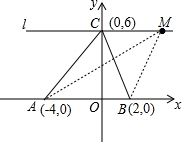
设M（a，6），
∵直线l平行于x轴，
∴△ABC和△MAB的边AB上的高相等为6，
∴△ABC和△MAB同底AB=6，等高为6，
∴S△ABC=S△MAB．
（3）P1（0，$\frac{21}{2}$），P2（0，$\frac{3}{2}$），P3（-7，0），P4（-1，0）．
点评 本题考查了坐标与图形性质，解决的关键是运用数形结合思想．
练习册系列答案
相关题目
如图，已知抛物线y=x2-2tx+t2-2的顶点A在第四象限，过点A作AB⊥y轴于点B，C是线段AB上一点（不与A、B重合），过点C作CD⊥x轴于点D，并交抛物线与点P．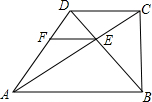
如图，直角梯形ABCD中，AB∥DC，∠ABC﹦90°，AD﹦BD，AC与BD相交于点E，AC⊥BD，过点E作EF∥AB交AD于F．
点P在数轴上运动，它所对应的数值为a，如图，当点P从点A运动到点B，则代数式$\sqrt{（a-1）^{2}}$+a+3的最大值为（ ）