题目内容
线段是中心对称图形,对称中心是它的中点; _____(判断对错)
 正确
【解析】因为线段绕它的中点旋转180度,可以和它本身重合.
故答案:正确.
正确
【解析】因为线段绕它的中点旋转180度,可以和它本身重合.
故答案:正确.
练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. 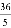 B.
B. 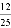 C.
C.  D.
D. 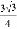
 A
【解析】试题分析:首先根据勾股定理可得:AB=,根据等面积法可得:点C到AB的距离为:(9×12)÷15=.
A
【解析】试题分析:首先根据勾股定理可得:AB=,根据等面积法可得:点C到AB的距离为:(9×12)÷15=. 如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
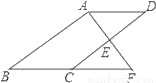
 (1)证明过程见解析;(2)8.
【解析】试题分析:(1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
试题解析:(1)∵四边形ABCD是平行四边形, ∴AD∥BC,AB∥CD,
...
(1)证明过程见解析;(2)8.
【解析】试题分析:(1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
试题解析:(1)∵四边形ABCD是平行四边形, ∴AD∥BC,AB∥CD,
... 如图,点D在BC上,DE⊥AB,DF⊥AC,垂足分别为E、F,DE=DF.求证:AD垂直平分EF.
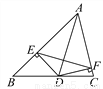
 见解析
【解析】试题分析:根据直角三角形的判定定理证明Rt△AED≌Rt△AFD,得到AE=AF,根据线段垂直平分线的判定定理证明结论.
试题解析:
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
又∵DE=DF,
∴AD是EF的垂直平分线,即AD垂直平分EF.
见解析
【解析】试题分析:根据直角三角形的判定定理证明Rt△AED≌Rt△AFD,得到AE=AF,根据线段垂直平分线的判定定理证明结论.
试题解析:
在Rt△AED和Rt△AFD中,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
又∵DE=DF,
∴AD是EF的垂直平分线,即AD垂直平分EF. 如何作出一个图形的中心对称图形?
 首先要先找到对称中心,对称点的连线一定经过对称中心,再就是两个图形是全等图形
【解析】【试题分析】本题目作一个图形的中心对称图形,方法见解析.
【试题解析】
首先要先找到对称中心,再将每个顶点与对称中心相连,并延长至等长,最后将得到每个对应点顺次连接即可.
首先要先找到对称中心,对称点的连线一定经过对称中心,再就是两个图形是全等图形
【解析】【试题分析】本题目作一个图形的中心对称图形,方法见解析.
【试题解析】
首先要先找到对称中心,再将每个顶点与对称中心相连,并延长至等长,最后将得到每个对应点顺次连接即可. 关于点O成中心对称的两个四边形ABCD和DEFG,AD、BE、CF、DG都过______
 点O
【解析】对应点的连线经过对称中心.
故答案:点O.
点O
【解析】对应点的连线经过对称中心.
故答案:点O. 下列图形中,是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
 A
【解析】根据中心对称的定义可知只有A选项符合,故选A.
A
【解析】根据中心对称的定义可知只有A选项符合,故选A. 在括号内填上适当的因式:
(1)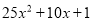 =(______); (2)
=(______); (2)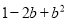 =(_____)
=(_____)
(3)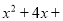 (_____)=(x+__)² (4)
(_____)=(x+__)² (4)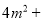 (____)+9n²=(_____)²
(____)+9n²=(_____)²
 (1)5x+1; (2)b-1 (3)4, 2 (4)±12mn; 2m±3n;
【解析】试题解析:(1)25x2+10x+1=(5x+1)2;
(2)1-2b+b2=(b-1)2
(3)x2+4x+4=(x+2)2;
(4)4m2+(±12mn)+9n2=(2m±3n)2.
故答案为:(5x+1),(b-1),4,2,±12mn,(2m±3n).
(1)5x+1; (2)b-1 (3)4, 2 (4)±12mn; 2m±3n;
【解析】试题解析:(1)25x2+10x+1=(5x+1)2;
(2)1-2b+b2=(b-1)2
(3)x2+4x+4=(x+2)2;
(4)4m2+(±12mn)+9n2=(2m±3n)2.
故答案为:(5x+1),(b-1),4,2,±12mn,(2m±3n). 若将点A(1,3)向左平移2个单位,再向下平移4个单位得到B,则点B的坐标为( )
A. (-2,-1) B. (-1,0) C. (-1,-1) D. (-2,0)
 C
【解析】∵点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,
∴点B的横坐标为1?2=?1,纵坐标为3?4=?1,
∴B的坐标为(?1,?1).
故选C.
C
【解析】∵点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,
∴点B的横坐标为1?2=?1,纵坐标为3?4=?1,
∴B的坐标为(?1,?1).
故选C. 
