题目内容
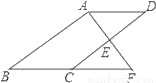
如图，E是?ABCD的边CD的中点，延长AE交BC的延长线于点F．
（1）求证：△ADE≌△FCE．
（2）若∠BAF=90°，BC=5，EF=3，求CD的长．
（1）证明过程见解析；（2）8.
【解析】试题分析：（1）由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE=∠F，∠D=∠ECF，由AAS证明△ADE≌△FCE即可；（2）由全等三角形的性质得出AE=EF=3，由平行线的性质证出∠AED=∠BAF=90°，由勾股定理求出DE，即可得出CD的长．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AD∥BC，AB∥CD，
...
练习册系列答案
相关题目
当分式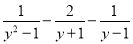
的值等于零时，则y=_________．
【解析】试题分析：当分式的值等于零时，
＝0，
去分母得：1－2(y－1)－(y＋1)＝0，
解得：y＝，
当y＝时y2－1≠0，
所以y＝是分式方程的解，
故答案为： ． 在△MNB中，BN=6，点A，C，D分别在MB，NB，MN上，四边形ABCD为平行四边形，且∠NDC=∠MDA，则四边形ABCD的周长是（ ）
A．24 B．18 C．16 D．12
D
【解析】
在平行四边形ABCD中CD∥AB，AD∥BC，∴∠M=∠NDC，∠N=∠MDA，∵∠NDC=
∠MDA，∴∠M=∠N=∠NDC=∠MDA，∴MB=BN=6，CD=CN，AD=MA，∴四边形ABCD的周长=AB+BC+CD+AD=MA+AB+BC+CN=MB+BN=2BN=12． “任意买一张电影票，座位号是2的倍数”，此事件是（ ）
A. 不可能事件 B. 不确定事件 C. 必然事件 D. 以上都不是
B
【解析】试题分析：因为电影票的座位号可能是奇数，也可能是偶数，所以任意买一张电影票，座位号是2的倍数，可能发生也可能不发生，所以此事件是不确定事件，故选：B． 今天下雨，两天后（ ）下雨.
A. 一定 B. 可能 C. 不可能 D. 以上都不对
B
【解析】今天下雨与两天后下雨不下雨没有任何关联.所以“两天后下雨”这是一个随机事件.
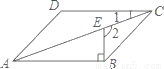
故选B. 如图，在?ABCD中，BE⊥AB交对角线AC于点E，若∠1=20°，则∠2的度数为__．
110°.
【解析】根据平行四边形的性质可得AB∥CD，根据平行线的性质可得∠1=∠CAB=20°，因BE⊥AB，可得∠EBA=90°，所以∠2=∠EBA+∠CAB=90°+20°=110°. 如图，已知线段AB。
（1）用尺规作图的方法作出线段AB的垂直平分线l（保留作图痕迹，不要求写出作法）；
（2）在（1）中所作的直线l上任意取两点M、N（线段AB的上方），连接AM、AN。BM、BN。
求证：∠MAN=∠MBN。
【解析】
（1）作图如下：
（2）证明：根据题意作出图形如图，
∵点M、N在线段AB的垂直平分线l上，
∴AM=BM，AN=BN。
又 ∵MN=MN，∴△AMN≌△BMN（SSS）。
∴∠MAN=∠MBN。
【解析】（1）根据线段垂直平分线的性质作图。
（2）根据线段垂直平分线上的点到线段两端距离相等的性质，可得AM=BM，AN=BN。MN是公共边，从而... 线段是中心对称图形，对称中心是它的中点； _____（判断对错）
正确
【解析】因为线段绕它的中点旋转180度，可以和它本身重合.
故答案：正确. 若非零实数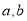
满足
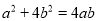，则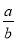
的值为（ ）
A. －2 B. 2 C.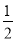 
D. 
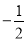
B
【解析】试题解析：把a2+4b2=4ab，变形得：（）2-4•+4=0，即（-2）2=0，
解得： =2，
故选B