题目内容
若将点A(1，3)向左平移2个单位，再向下平移4个单位得到B，则点B的坐标为( )
A. (－2，－1) B. (－1，0) C. (－1，－1) D. (－2，0)
C
【解析】∵点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，
∴点B的横坐标为1?2＝?1，纵坐标为3?4＝?1，
∴B的坐标为（?1，?1）．
故选C．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
线段是中心对称图形，对称中心是它的中点； _____（判断对错）
正确
【解析】因为线段绕它的中点旋转180度，可以和它本身重合.
故答案：正确. 若非零实数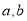
满足
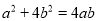，则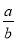
的值为（ ）
A. －2 B. 2 C.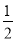 
D.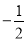 
B
【解析】试题解析：把a2+4b2=4ab，变形得：（）2-4•+4=0，即（-2）2=0，
解得： =2，
故选B 将点A（﹣2，﹣3）向右平移3个单位长度得到点B，则点B所处的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
D
【解析】点A(－2，－3)向右平移3个单位长度所得到的点B的坐标为(1，－3)，故点B在第四象限． 将四边形ABCD平移后得到四边形A′B′C′D′，已知点A(－1,2)的对应点为A′(－7,10)．若将四边形A′B′C′D′看成由四边形ABCD沿A到A′的方向一次平移得到的，则平移的距离为____.
10
【解析】因为平移后点A(－1,2)的对应点为A′(－7,10),即点A先向左平移了6个单位,向上平移了8个单位,根据勾股定理可得A A′,故答案为:10. 已知二次函数y=x2+2x+c的图象经过点（1，-5）．
（1）求c的值；
（2）求函数图象与x轴的交点坐标．
（1）8；（2）（-4，0），（2，0）
【解析】试题分析：（1）二次函数解析式只有一个待定系数c，把点（1，-5）代入解析式即可求c；
（2）已知二次函数解析式求函数图象与x轴的交点坐标，令y=0，解一元二次方程，可得交点的横坐标．
试题分析：（1）∵点（1，-5）在y=x2+2x+c的图象上，
∴-5=1+2+c，
∴c= -8；
（2）令y=0，则x2+2... 已知二次函数y=﹣x2+2x+m的部分图象如图所示，则关于x的一元二次方程﹣x2+2x+m=0的解为_____．
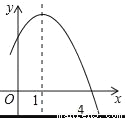
x1=4，x2=﹣2
【解析】试题分析：由二次函数y=﹣x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标，然后可以求出另一个交点坐标，再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程﹣x2+2x+m=0的解．
【解析】
依题意得二次函数y=﹣x2+2x+m的对称轴为x=1，与x轴的一个交点为（3，0），
∴抛物线... 因式分【解析】
（1）20a3﹣30a2
（2）16﹣（2a+3b）2
（3）﹣16x2y2+12xy3z
（4）5x2y﹣25x2y2+40x3y
（5）x2（a﹣b）2﹣y2（b﹣a）2
（6）（a2+b2）2﹣4a2b2
（7）18b（a﹣b）2+12（b﹣a）3
（8）x（x2+1）2﹣4x3
（9）（x2﹣2x）2﹣3（x2﹣2x）
（10）（2x﹣1）2﹣6（2x﹣1）+9
（11）16x4﹣72x2y2+81y4
（12）a5﹣a
（13）25（x+y）2﹣9（x﹣y）2
（14）m2﹣3m﹣28
（15）x2+x﹣20．
（1）10a2（2a﹣3）；（2）（4+2a+3b）（4﹣2a﹣3b）；
（3）﹣4xy2（4x﹣3yz）；
（4）5x2y（1﹣5y+8x）；
（5）（a﹣b）2（x+y）（x﹣y）；
（6）（a+b）2（a﹣b）2；
（7）6（b﹣a）2（5b﹣2a）；
（8）x（x+1）2（x﹣1）2；
（9）x（x﹣2）（x﹣3）（x+1）；
（10）4（x... 如图，在△ABC中，∠B≠∠C.求证：AB≠AC.
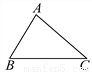
见解析
【解析】试题分析：首先假设AB=AC，从而得出与已知条件矛盾，从而得出答案．
试题解析：假设AB=AC， 则∠B=∠C，∴与已知矛盾，∴AB≠AC．