题目内容
如何作出一个图形的中心对称图形?
 首先要先找到对称中心,对称点的连线一定经过对称中心,再就是两个图形是全等图形
【解析】【试题分析】本题目作一个图形的中心对称图形,方法见解析.
【试题解析】
首先要先找到对称中心,再将每个顶点与对称中心相连,并延长至等长,最后将得到每个对应点顺次连接即可.
首先要先找到对称中心,对称点的连线一定经过对称中心,再就是两个图形是全等图形
【解析】【试题分析】本题目作一个图形的中心对称图形,方法见解析.
【试题解析】
首先要先找到对称中心,再将每个顶点与对称中心相连,并延长至等长,最后将得到每个对应点顺次连接即可.
练习册系列答案
相关题目
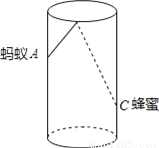
如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为__cm.
 5
【解析】试题分析:沿过A的圆柱的高剪开,得出矩形EFGH,过C作CQ⊥EF于Q,作A关于EH的对称点,连接交EH于P,连接AP,
则AP+PC就是蚂蚁到达蜂蜜的最短距离,∵AE= , =AP,∴AP+PC= +PC= ,∵CQ=×18=9cm, =12-4+4=12cm,在Rt△中,由勾股定理得: ==15cm.故答案为15.
5
【解析】试题分析:沿过A的圆柱的高剪开,得出矩形EFGH,过C作CQ⊥EF于Q,作A关于EH的对称点,连接交EH于P,连接AP,
则AP+PC就是蚂蚁到达蜂蜜的最短距离,∵AE= , =AP,∴AP+PC= +PC= ,∵CQ=×18=9cm, =12-4+4=12cm,在Rt△中,由勾股定理得: ==15cm.故答案为15. 今天下雨,两天后( )下雨.
A. 一定 B. 可能 C. 不可能 D. 以上都不对
 B
【解析】今天下雨与两天后下雨不下雨没有任何关联.所以“两天后下雨”这是一个随机事件.
故选B.
B
【解析】今天下雨与两天后下雨不下雨没有任何关联.所以“两天后下雨”这是一个随机事件.
故选B. 如图,已知线段AB。

(1)用尺规作图的方法作出线段AB的垂直平分线l(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线l上任意取两点M、N(线段AB的上方),连接AM、AN。BM、BN。
求证:∠MAN=∠MBN。
 【解析】
(1)作图如下:
(2)证明:根据题意作出图形如图,
∵点M、N在线段AB的垂直平分线l上,
∴AM=BM,AN=BN。
又 ∵MN=MN,∴△AMN≌△BMN(SSS)。
∴∠MAN=∠MBN。
【解析】(1)根据线段垂直平分线的性质作图。
(2)根据线段垂直平分线上的点到线段两端距离相等的性质,可得AM=BM,AN=BN。MN是公共边,从而...
【解析】
(1)作图如下:
(2)证明:根据题意作出图形如图,
∵点M、N在线段AB的垂直平分线l上,
∴AM=BM,AN=BN。
又 ∵MN=MN,∴△AMN≌△BMN(SSS)。
∴∠MAN=∠MBN。
【解析】(1)根据线段垂直平分线的性质作图。
(2)根据线段垂直平分线上的点到线段两端距离相等的性质,可得AM=BM,AN=BN。MN是公共边,从而... 在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B等于_____.
 6种
【解析】试题分析:当△ABC是锐角三角形时,则∠B=70°,当△ABC是钝角三角形时,则∠B=20°.
6种
【解析】试题分析:当△ABC是锐角三角形时,则∠B=70°,当△ABC是钝角三角形时,则∠B=20°. 线段是中心对称图形,对称中心是它的中点; _____(判断对错)
 正确
【解析】因为线段绕它的中点旋转180度,可以和它本身重合.
故答案:正确.
正确
【解析】因为线段绕它的中点旋转180度,可以和它本身重合.
故答案:正确. 关于中心对称的两个图形,对称点的连线经过__________
 对称中心
【解析】关于中心对称的两个图形,对称点的连线经过对称中心.
故答案:对称中心.
对称中心
【解析】关于中心对称的两个图形,对称点的连线经过对称中心.
故答案:对称中心. 分解因式:
(1)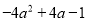 (2)
(2) 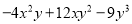
(3)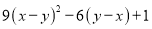 (4)
(4) 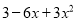
(5)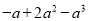 (6)
(6) 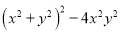
(7)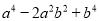 8)
8)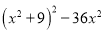
(9)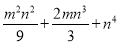 (10)
(10)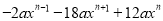
 (1)-(2a-1)2;(2)-y(2x-3y)2;(3)(3x-3y+1)2;(4)3(1-x)2;(5)-a(1-a)2;
(6)(x+y)2(x-y)2; (7)(a+b)2(a-b)2; (8)(x+3)2(x-3)2; (9) ;(10) .
【解析】试题分析:(1)首先提取负号,再利用完全平方公式进行分解;
(2)首先提取公因式-y,再利用完全平方公式进行分解;
...
(1)-(2a-1)2;(2)-y(2x-3y)2;(3)(3x-3y+1)2;(4)3(1-x)2;(5)-a(1-a)2;
(6)(x+y)2(x-y)2; (7)(a+b)2(a-b)2; (8)(x+3)2(x-3)2; (9) ;(10) .
【解析】试题分析:(1)首先提取负号,再利用完全平方公式进行分解;
(2)首先提取公因式-y,再利用完全平方公式进行分解;
... 将四边形ABCD平移后得到四边形A′B′C′D′,已知点A(-1,2)的对应点为A′(-7,10).若将四边形A′B′C′D′看成由四边形ABCD沿A到A′的方向一次平移得到的,则平移的距离为____.
 10
【解析】因为平移后点A(-1,2)的对应点为A′(-7,10),即点A先向左平移了6个单位,向上平移了8个单位,根据勾股定理可得A A′,故答案为:10.
10
【解析】因为平移后点A(-1,2)的对应点为A′(-7,10),即点A先向左平移了6个单位,向上平移了8个单位,根据勾股定理可得A A′,故答案为:10. 
