题目内容
关于点O成中心对称的两个四边形ABCD和DEFG，AD、BE、CF、DG都过______
点O
【解析】对应点的连线经过对称中心.
故答案：点O.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知平行四边形ABCD，DE是∠ADC的角平分线，交BC于点E．
（1）求证：CD=CE；
（2）若BE=CE，∠B=80°，求∠DAE的度数．
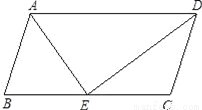
（1）证明见解析；（2）∠DAE=50°．
【解析】试题分析:（1）根据DE是∠ADC的角平分线得到∠1=∠2，再根据平行四边形的性质得到∠1=∠3，所以∠2=∠3，根据等角对等边即可得证；
（2）先根据BE=CE结合CD=CE得到△ABE是等腰三角形，求出∠BAE的度数，再根据平行四边形邻角互补得到∠BAD=100°，所以∠DAE可求．
（1）证明：如图，在平行四边形ABCD中... 如图，在?ABCD中，BE⊥AB交对角线AC于点E，若∠1=20°，则∠2的度数为__．
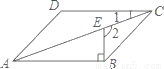
110°.
【解析】根据平行四边形的性质可得AB∥CD，根据平行线的性质可得∠1=∠CAB=20°，因BE⊥AB，可得∠EBA=90°，所以∠2=∠EBA+∠CAB=90°+20°=110°. 如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为( )
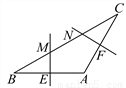
A. 4cm B. 3cm C. 2cm D. 1cm
C
【解析】连接AM、AN、过A作AD⊥BC于D，如图所示：
∵在△ABC中，AB=AC，∠A=120°，BC=6cm，
∴∠B=∠C=30°，BD=CD=3cm，
∴AB= cm=AC，
∵AB的垂直平分线EM，
∴BE= AB= cm
同理CF=cm，
∴BM==2cm，
同理CN=2cm，
∴MN=BC-BM-CN=2cm，
故选C． 线段是中心对称图形，对称中心是它的中点； _____（判断对错）
正确
【解析】因为线段绕它的中点旋转180度，可以和它本身重合.
故答案：正确. 圆是中心对称图形，它的对称中心是( )
A. 圆周 B. 圆心 C. 半径 D. 直径
B
【解析】圆的是既是中心对称图形又是轴对称图形，对称中心是圆心.故选B. 下列图形中是轴对称而不是中心对称图形的是（ ）
A. 平行四边形
B. 线段
C. 角
D. 正方形
C
【解析】试题解析：平行四边形的对称中心为两条对角线的交点，不是轴对称图形；线段的对称中心为线段的中点，对称轴为线段的中垂线；角不是中心对称图形，对称轴为角平分线所在直线；正方形的对称中心为两条对角线的交点，对称轴为两条对角线所在直线及两条对边中点连线所在直线；所以选择C． 已知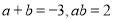
，则(a-b) ²的值是（ ）
A. 1 B. 4 C. 16 D. 9
A
【解析】试题解析：∵a+b=-3，ab=2，
∴（a-b）2=a2+b2-2ab，
=a2+b2+2ab-4ab，
=（a+b）2-4ab，
=（-3）2-4×2，
=9-8，
=1．
故选A． 已知二次函数y=x2+2x+c的图象经过点（1，-5）．
（1）求c的值；
（2）求函数图象与x轴的交点坐标．
（1）8；（2）（-4，0），（2，0）
【解析】试题分析：（1）二次函数解析式只有一个待定系数c，把点（1，-5）代入解析式即可求c；
（2）已知二次函数解析式求函数图象与x轴的交点坐标，令y=0，解一元二次方程，可得交点的横坐标．
试题分析：（1）∵点（1，-5）在y=x2+2x+c的图象上，
∴-5=1+2+c，
∴c= -8；
（2）令y=0，则x2+2...