题目内容
 如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.
如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.(1)求证:△BDE是等腰三角形.
(2)当∠BCD=
考点:直角三角形斜边上的中线,等腰三角形的判定,等腰直角三角形
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得BE=DE=
AC,再根据等腰三角形的定义判定即可;
(2)根据等边对等角可得∠CBE=∠ACB,∠DCE=∠CDE,再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可.
| 1 |
| 2 |
(2)根据等边对等角可得∠CBE=∠ACB,∠DCE=∠CDE,再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可.
解答:(1)证明:∵∠ABC=∠ADC=90°,E是对角线AC的中点,
∴BE=DE=CE=
AC,
∴△BDE是等腰三角形;
(2)解:∵BE=CE=DE,
∴∠CBE=∠ACB,∠DCE=∠CDE,
由三角形的外加性质得,∠AEB=∠ACB+∠CBE=2∠ACB,
∠AED=∠CDE+∠DCE=2∠DCE,
∴∠BED=∠AEB+∠AED=2(∠ACB+∠DCE)=2∠BCD,
∵△BDE是等腰直角三角形,
∴∠BED=90°,
∴2∠BCD=90°,
∴∠BCD=45°.
故答案为:45.
∴BE=DE=CE=
| 1 |
| 2 |
∴△BDE是等腰三角形;
(2)解:∵BE=CE=DE,
∴∠CBE=∠ACB,∠DCE=∠CDE,
由三角形的外加性质得,∠AEB=∠ACB+∠CBE=2∠ACB,
∠AED=∠CDE+∠DCE=2∠DCE,
∴∠BED=∠AEB+∠AED=2(∠ACB+∠DCE)=2∠BCD,
∵△BDE是等腰直角三角形,
∴∠BED=90°,
∴2∠BCD=90°,
∴∠BCD=45°.
故答案为:45.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,等腰直角三角形的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
小明利用计算机设计了一个计算程序,输入和输出的数据为下表:
那么,当输入数据是9时,输出的数据是( )
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … | ||||||||||
| 输出 | … |
|
|
|
|
| … |
A、
| ||
B、
| ||
C、
| ||
D、
|
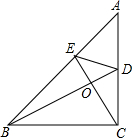 如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证:
如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证: 已知,如图,平行四边形ABCD中,∠BDC的平分线DE交直线AB于E,取DE中点M并连接CM、BM.
已知,如图,平行四边形ABCD中,∠BDC的平分线DE交直线AB于E,取DE中点M并连接CM、BM. 下图是一个长方形纸片,长为5a2+4b2,宽为6a2,在它的四个角上都剪去一个边长为
下图是一个长方形纸片,长为5a2+4b2,宽为6a2,在它的四个角上都剪去一个边长为
 如图,AE是位于公路边的电线杆,高为12m,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根为6m的水泥撑杆BD,用于撑起电线.已知两根杆子之间的距离为8m,电线CD与水平线AC的夹角为60°.求电线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计).
如图,AE是位于公路边的电线杆,高为12m,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根为6m的水泥撑杆BD,用于撑起电线.已知两根杆子之间的距离为8m,电线CD与水平线AC的夹角为60°.求电线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计).