题目内容
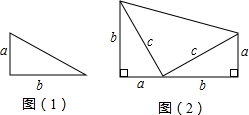
 如图,AE是位于公路边的电线杆,高为12m,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根为6m的水泥撑杆BD,用于撑起电线.已知两根杆子之间的距离为8m,电线CD与水平线AC的夹角为60°.求电线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计).
如图,AE是位于公路边的电线杆,高为12m,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根为6m的水泥撑杆BD,用于撑起电线.已知两根杆子之间的距离为8m,电线CD与水平线AC的夹角为60°.求电线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计).考点:解直角三角形的应用
专题:
分析:作DF⊥AE于点F,则四边形ABDF是矩形,在直角△DEF中利用勾股定理求得DE的长,然后在直角△BCD中利用三角函数求得DC的长,则ED+DC即是所求.
解答: 解:作DF⊥AE于点F,则四边形ABDF是矩形.DF=AB=8(米),
解:作DF⊥AE于点F,则四边形ABDF是矩形.DF=AB=8(米),
EF=AE-AF=AE-BD=12-6=6(m)..
在直角△DEF中,DE=
=
=10(m).
在直角△BCD中,sin∠DCB=
,
则DC=
=
BD=2
(m).
则电线CDE的总长L=DE+DC=10+2
(m).
答:电线CDE的总长L是(10+2
)m.
 解:作DF⊥AE于点F,则四边形ABDF是矩形.DF=AB=8(米),
解:作DF⊥AE于点F,则四边形ABDF是矩形.DF=AB=8(米),EF=AE-AF=AE-BD=12-6=6(m)..
在直角△DEF中,DE=
| EF2+DF2 |
| 82+62 |
在直角△BCD中,sin∠DCB=
| BD |
| DC |
则DC=
| BD |
| tan60° |
| ||
| 3 |
| 3 |
则电线CDE的总长L=DE+DC=10+2
| 3 |
答:电线CDE的总长L是(10+2
| 3 |
点评:此题考查了三角函数的基本概念,主要是正弦概念及运算,关键把实际问题转化为数学问题加以计算.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
下列运算正确的是( )
| A、а2•а3=а6 |
| B、(-а2)3=-а6 |
| C、(аb)2=аb2 |
| D、а6÷а3=а2 |
 如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.
如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.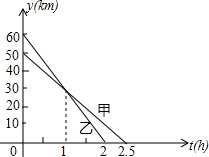 甲乙两人在一笔直的公路上,沿同一方向骑自行车同时出发前往A地,到A地后停止,他们距A地的路程ykm与甲行驶的时间x小时之间的关系如图所示,则出发
甲乙两人在一笔直的公路上,沿同一方向骑自行车同时出发前往A地,到A地后停止,他们距A地的路程ykm与甲行驶的时间x小时之间的关系如图所示,则出发