题目内容
 已知,如图,平行四边形ABCD中,∠BDC的平分线DE交直线AB于E,取DE中点M并连接CM、BM.
已知,如图,平行四边形ABCD中,∠BDC的平分线DE交直线AB于E,取DE中点M并连接CM、BM.(1)直接写出线段BM和DE的位置关系.
(2)若BD=2DC,则△DCM的形状是
考点:平行四边形的性质
专题:
分析:(1)由平行四边形ABCD中,∠BDC的平分线DE交直线AB于E,易证得△BDE是等腰三角形,又由取DE中点M,根据三线合一的性质,可得BM⊥DE;
(2)首先取BD的中点N,连接MN,由三角形中位线的性质与直角三角形的性质,易证得四边形CDNM是菱形,继而可得△DCM是等腰三角形.
(2)首先取BD的中点N,连接MN,由三角形中位线的性质与直角三角形的性质,易证得四边形CDNM是菱形,继而可得△DCM是等腰三角形.
解答: 解:(1)BM⊥DE.
解:(1)BM⊥DE.
理由:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠CDE=∠E,
∵DE平分∠BDC,
∴∠BDE=∠CDE,
∴∠BDE=∠E,
∴BD=BE,
∵M是DE中点,
∴BM⊥DE;
(2)△DCM是等腰三角形.
理由:取BD的中点N,连接MN,
∵BM⊥DE,
∴MN=DN=
BD,
∵BD=2CD,
∴CD=DN=MN,
∵M是DE的中点,
∴MN∥BE,
∵AB∥CD,
∴MN∥CD,
∴四边形CDNM是平行四边形,
∴?CDNM是菱形,
∴CD=CM.
∴△DCM是等腰三角形.
 解:(1)BM⊥DE.
解:(1)BM⊥DE.理由:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠CDE=∠E,
∵DE平分∠BDC,
∴∠BDE=∠CDE,
∴∠BDE=∠E,
∴BD=BE,
∵M是DE中点,
∴BM⊥DE;
(2)△DCM是等腰三角形.
理由:取BD的中点N,连接MN,
∵BM⊥DE,
∴MN=DN=
| 1 |
| 2 |
∵BD=2CD,
∴CD=DN=MN,
∵M是DE的中点,
∴MN∥BE,
∵AB∥CD,
∴MN∥CD,
∴四边形CDNM是平行四边形,
∴?CDNM是菱形,
∴CD=CM.
∴△DCM是等腰三角形.
点评:此题考查了平行四边形的性质、等腰三角形的性质以及直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
若am+1b3和(n-1)a2b3与是同类项,且它们合并后结果是0,则( )
| A、m=2,n=2 |
| B、m=1,n=2 |
| C、m=2,n=0 |
| D、m=1,n=0 |
在-2,-|-6|,-(-5),-32,(-2)2,2-1,(-1)0中正数的个数为( )
| A、2个 | B、3个 | C、4个 | D、5个 |
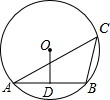 如图所示,已知△ABC内接于⊙O,∠C=45°,点O到弦AB的距离OD=2,求:
如图所示,已知△ABC内接于⊙O,∠C=45°,点O到弦AB的距离OD=2,求: 已知直线a,b,过a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a于点C.则点B到直线a的距离是
已知直线a,b,过a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a于点C.则点B到直线a的距离是 如图,已知∠1=∠2,∠B=80°,求∠BCD的度数.
如图,已知∠1=∠2,∠B=80°,求∠BCD的度数. 如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.
如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.