题目内容
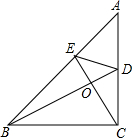 如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证:
如图,在△ABC中,∠ACB=90°,BD是∠ABC的平分线,E为AB边上一点,且CE⊥BD,垂足为O,求证:(1)BD是线段CE的垂直平分线.
(2)∠ADE=∠ABC.
考点:线段垂直平分线的性质
专题:证明题
分析:(1)由条件可证明△BOE≌△BOC,可证得BE=BC,再证明△BDE≌△BDC,可证得DE=DC,可证得结论;
(2)结合(1)可证明∠AED=∠ACB=90°,可证明∠ADE=∠ABC.
(2)结合(1)可证明∠AED=∠ACB=90°,可证明∠ADE=∠ABC.
解答:证明:(1)∵BD平分∠ABC,
∴∠EBO=∠CBO,
∵CE⊥BD,
∴∠BOE=∠BOC,
在△BOE和△BOC中,
,
∴△BOE≌△BOC(ASA),
∴BE=BC,
在△BDE和△BDC中,
,
∴△BDE≌△BDC(SAS),
∴DE=DC,
∴点B、D都在线段AC的垂直平分线上,
∴BD是线段CE的垂直平分线;
(2)由(1)可知△BDE≌△BDC,
∴∠BED=∠ACB=90°,
∴∠A+∠ADE=∠A+∠ABC,
∴∠ADE=∠ABC.
∴∠EBO=∠CBO,
∵CE⊥BD,
∴∠BOE=∠BOC,
在△BOE和△BOC中,
|
∴△BOE≌△BOC(ASA),
∴BE=BC,
在△BDE和△BDC中,
|
∴△BDE≌△BDC(SAS),
∴DE=DC,
∴点B、D都在线段AC的垂直平分线上,
∴BD是线段CE的垂直平分线;
(2)由(1)可知△BDE≌△BDC,
∴∠BED=∠ACB=90°,
∴∠A+∠ADE=∠A+∠ABC,
∴∠ADE=∠ABC.
点评:本题主要考查线段垂直平分线的判定和性质,掌握到线段两端点距离相等的点在线段的垂直平分线上是解题的关键.

练习册系列答案
相关题目
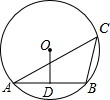 如图所示,已知△ABC内接于⊙O,∠C=45°,点O到弦AB的距离OD=2,求:
如图所示,已知△ABC内接于⊙O,∠C=45°,点O到弦AB的距离OD=2,求: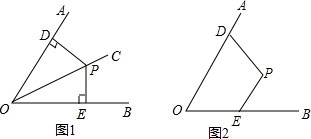
 在一次黑板报的评选中,九年级(1)班获得了第一名,其中小颖同学的图案得到了大家的一致好评.她设计的图案是由如图所示的三角形图案绕上面的点O按同一个方向依次旋转90°,180°,270°得到的图形组成的,请你画出这个图案,并描述这个图案像什么.
在一次黑板报的评选中,九年级(1)班获得了第一名,其中小颖同学的图案得到了大家的一致好评.她设计的图案是由如图所示的三角形图案绕上面的点O按同一个方向依次旋转90°,180°,270°得到的图形组成的,请你画出这个图案,并描述这个图案像什么. 已知直线a,b,过a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a于点C.则点B到直线a的距离是
已知直线a,b,过a上一点A作AB⊥a,交b于点B,过B作BC⊥b交a于点C.则点B到直线a的距离是 如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.
如图,四边形ABCD中,∠ABC=∠ADC=90°,E是对角线AC的中点,连接BE、DE.