题目内容
(1)观察下列式子:
=
=
-
;
=
=
-
;
=
=
-
;
=
=
-
;…
由此可以推测:
= ,
= ;
(2)请猜想出能表示出(1)的特点的一般规律,用含字母n的等式表示出来(n为正整数),并证明;
(3)请用(2)中的规律计算:
-
+
.
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 20 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
由此可以推测:
| 1 |
| 42 |
| 1 |
| 72 |
(2)请猜想出能表示出(1)的特点的一般规律,用含字母n的等式表示出来(n为正整数),并证明;
(3)请用(2)中的规律计算:
| 1 |
| (x-2)(x-3) |
| 2 |
| (x-1)(x-3) |
| 1 |
| (x-1)(x-2) |
考点:规律型:数字的变化类
专题:规律型
分析:(1)
可化为6与7的倒数之差;
可化为8与9的倒数之差;
(2)观察(1)的各式,每个分数的分母为两个连续的整数之积,则这个分数等于两整数的倒数之差;
(3)利用(2)中规律展开得到原式=
-
-(
-
)+
-
,然后去括号合并即可.
| 1 |
| 42 |
| 1 |
| 72 |
(2)观察(1)的各式,每个分数的分母为两个连续的整数之积,则这个分数等于两整数的倒数之差;
(3)利用(2)中规律展开得到原式=
| 1 |
| x-2 |
| 1 |
| x-3 |
| 1 |
| x-1 |
| 1 |
| x-3 |
| 1 |
| x-1 |
| 1 |
| x-2 |
解答:解:(1)
=
=
-
;
=
=
-
.
故答案为
=
-
;
=
-
;
(2)一般规律为
=
-
(n≥1的整数).
证明:
-
=
-
=
;
(3)原式=
-
-(
-
)+
-
=
-
-
+
+
-
=0
| 1 |
| 42 |
| 1 |
| 6×7 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 72 |
| 1 |
| 8×9 |
| 1 |
| 8 |
| 1 |
| 9 |
故答案为
| 1 |
| 42 |
| 1 |
| 6 |
| 1 |
| 7 |
| 1 |
| 72 |
| 1 |
| 8 |
| 1 |
| 9 |
(2)一般规律为
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
证明:
| 1 |
| n |
| 1 |
| n+1 |
| n+1 |
| n(n+1) |
| n |
| n(n+1) |
| 1 |
| n(n+1) |
(3)原式=
| 1 |
| x-2 |
| 1 |
| x-3 |
| 1 |
| x-1 |
| 1 |
| x-3 |
| 1 |
| x-1 |
| 1 |
| x-2 |
=
| 1 |
| x-2 |
| 1 |
| x-3 |
| 1 |
| x-1 |
| 1 |
| x-3 |
| 1 |
| x-1 |
| 1 |
| x-2 |
=0
点评:通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.

练习册系列答案
相关题目

 如图,AB、CD是⊙O中互相垂直的两条直径,以A为圆心,OA为半径画弧,与⊙O交于E、F两点.
如图,AB、CD是⊙O中互相垂直的两条直径,以A为圆心,OA为半径画弧,与⊙O交于E、F两点.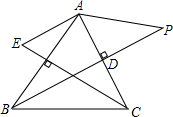 如图,在△ABC中,BD⊥AC,CE⊥AB,在射线BD上取一点P,使BP=kAC,在射线CF上取一点E,使∠AEC+∠BAP=180°.探究AP与AE的数量关系.
如图,在△ABC中,BD⊥AC,CE⊥AB,在射线BD上取一点P,使BP=kAC,在射线CF上取一点E,使∠AEC+∠BAP=180°.探究AP与AE的数量关系.