题目内容
已知∠AOB=100°,OC为一条射线,OD平分∠AOC,OE平分∠BOC.
(1)如图①,OC在∠AOB内部,且∠AOC=40°,求∠DOE的度数;
(2)在①中,若∠AOC=a,其余条件不变,求∠DOE的度数;
(3)如图②,OC在∠AOB外部,OD平分∠AOC,OE平分∠BOC,你能求出∠DOE的度数吗?若能,请求出∠DOE的度数,若不能,请说明理由.

(1)如图①,OC在∠AOB内部,且∠AOC=40°,求∠DOE的度数;
(2)在①中,若∠AOC=a,其余条件不变,求∠DOE的度数;
(3)如图②,OC在∠AOB外部,OD平分∠AOC,OE平分∠BOC,你能求出∠DOE的度数吗?若能,请求出∠DOE的度数,若不能,请说明理由.

考点:角的计算,角平分线的定义
专题:
分析:(1)由∠AOB=100°,∠AOC=40°,可得∠BOC=∠AOB-∠AOC=60°,然后由角平分线的定义可得:∠DOC=
∠AOC=20°,∠COE=
∠BOC=30°,然后利用两角的和差即可计算∠DOE的度数;
(2)由∠AOB=100°,∠AOC=α,可得∠BOC=∠AOB-∠AOC=100°-α,然后由角平分线的定义可得:∠DOC=
∠AOC=
α,∠COE=
∠BOC=
(100°-α),然后利用两角的和差即可计算∠DOE的度数;
(3)由OE平分∠BOC,所以∠BOE=∠COE,设∠BOE=∠COE=x°,可得∠AOC=∠AOB+∠BOC=100°+2x,因为OD平分∠AOC,所以∠AOD=∠DOC=
∠AOC=(50+x)°,
然后由∠DOE=∠DOC-∠COE,将∠DOC=(50+x)°,∠COE=x°代入即可.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由∠AOB=100°,∠AOC=α,可得∠BOC=∠AOB-∠AOC=100°-α,然后由角平分线的定义可得:∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由OE平分∠BOC,所以∠BOE=∠COE,设∠BOE=∠COE=x°,可得∠AOC=∠AOB+∠BOC=100°+2x,因为OD平分∠AOC,所以∠AOD=∠DOC=
| 1 |
| 2 |
然后由∠DOE=∠DOC-∠COE,将∠DOC=(50+x)°,∠COE=x°代入即可.
解答:解:(1)∵∠BOC=∠AOB-∠AOC,∠AOB=100°,∠AOC=40°,
∴∠BOC=100°-40°=60°,
∵OD平分∠AOC,OE平分∠BOC,
∴∠DOC=
∠AOC=20°,∠COE=
∠BOC=30°,
∵∠DOE=∠DOC+∠COE,
∴∠DOE=20°+30°=50°;
(2))∵∠BOC=∠AOB-∠AOC,∠AOB=100°,∠AOC=α,
∴∠BOC=100°-α,
∵OD平分∠AOC,OE平分∠BOC,
∴∠DOC=
∠AOC=
α,∠COE=
∠BOC=
(100°-α),
∵∠DOE=∠DOC+∠COE,
∴∠DOE=
α+
(100°-α)=50°;
(3)能求出∠DOE的度数,
理由如下:
∵OE平分∠BOC,
∴∠BOE=∠COE=
∠BOC,
设∠BOE=∠COE=x°,则∠BOC=2x°
∴∠AOC=∠AOB+∠BOC=100°+2x°,
∵OD平分∠AOC,
∴∠AOD=∠DOC=
∠AOC=(50+x)°,
∵∠DOE=∠DOC-∠COE,
∴∠DOE=(50+x)°-x°=50°.
∴∠BOC=100°-40°=60°,
∵OD平分∠AOC,OE平分∠BOC,
∴∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DOE=∠DOC+∠COE,
∴∠DOE=20°+30°=50°;
(2))∵∠BOC=∠AOB-∠AOC,∠AOB=100°,∠AOC=α,
∴∠BOC=100°-α,
∵OD平分∠AOC,OE平分∠BOC,
∴∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠DOE=∠DOC+∠COE,
∴∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
(3)能求出∠DOE的度数,
理由如下:
∵OE平分∠BOC,
∴∠BOE=∠COE=
| 1 |
| 2 |
设∠BOE=∠COE=x°,则∠BOC=2x°
∴∠AOC=∠AOB+∠BOC=100°+2x°,
∵OD平分∠AOC,
∴∠AOD=∠DOC=
| 1 |
| 2 |
∵∠DOE=∠DOC-∠COE,
∴∠DOE=(50+x)°-x°=50°.
点评:本题考查了角的平分线定义和角的有关计算的应用,主要考查学生计算能力和推理能力,求解过程类似.

练习册系列答案
相关题目
四个数-5,0,
,
中为无理数的是( )
| 1 |
| 2 |
| 3 |
| A、-5 | ||
| B、0 | ||
C、
| ||
D、
|
 如图,在△ABC中,AB=AC,O是AB上一点,以O为圆心的圆经过点A,交AB于点F,与BC相切于点E.点D为BC的中点,连结AD、OE、AE.
如图,在△ABC中,AB=AC,O是AB上一点,以O为圆心的圆经过点A,交AB于点F,与BC相切于点E.点D为BC的中点,连结AD、OE、AE.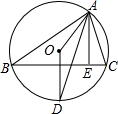 如图,O是△ABC的外心,D是圆上一点,且OD⊥BC,AE是BC边上的高.试探索∠OAD与∠EAD的大小关系,并说明理由.
如图,O是△ABC的外心,D是圆上一点,且OD⊥BC,AE是BC边上的高.试探索∠OAD与∠EAD的大小关系,并说明理由.