题目内容
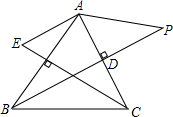 如图,在△ABC中,BD⊥AC,CE⊥AB,在射线BD上取一点P,使BP=kAC,在射线CF上取一点E,使∠AEC+∠BAP=180°.探究AP与AE的数量关系.
如图,在△ABC中,BD⊥AC,CE⊥AB,在射线BD上取一点P,使BP=kAC,在射线CF上取一点E,使∠AEC+∠BAP=180°.探究AP与AE的数量关系.考点:相似三角形的判定与性质
专题:
分析:延长BA,过P作PF⊥BA,设CE交AB于点O,可先证明△PFA∽△AOE,再证明△PFB∽△AOC,利用相似三角形的性质可得到AP和AE的数量关系.
解答: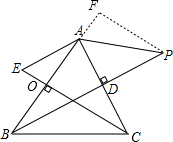 解:AP=kAE,证明如下:
解:AP=kAE,证明如下:
延长BA,过P作PF⊥BA,设CE交AB于点O,
∵∠AEC+∠BAP=180°,∠FAP+∠BAP=180°,
∴∠E=∠FAP,∠AOE=∠AFP=90°,
∴△PFA∽△AOE,
∴
=
,
∵AC⊥BD,AB⊥EC,
∴∠BAC+∠ABD=∠BAC+∠ECA=90°,
∴∠ABP=∠ACE,且∠PFB=∠AOC=90°,
∴△PFB∽△AOC,
∴
=
=k,
∴AP=kAE.
 解:AP=kAE,证明如下:
解:AP=kAE,证明如下:延长BA,过P作PF⊥BA,设CE交AB于点O,
∵∠AEC+∠BAP=180°,∠FAP+∠BAP=180°,
∴∠E=∠FAP,∠AOE=∠AFP=90°,
∴△PFA∽△AOE,
∴
| AP |
| AE |
| PF |
| AO |
∵AC⊥BD,AB⊥EC,
∴∠BAC+∠ABD=∠BAC+∠ECA=90°,
∴∠ABP=∠ACE,且∠PFB=∠AOC=90°,
∴△PFB∽△AOC,
∴
| AP |
| AE |
| BP |
| AC |
∴AP=kAE.
点评:本题主要考查相似三角形的判定和性质,过P作垂线构造△PFA∽△AOE是解题的关键,注意相似三角形的对应边成比例.

练习册系列答案
相关题目
在给定下面的四个图案中,位似图形有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在△ABC中,AB=AC,O是AB上一点,以O为圆心的圆经过点A,交AB于点F,与BC相切于点E.点D为BC的中点,连结AD、OE、AE.
如图,在△ABC中,AB=AC,O是AB上一点,以O为圆心的圆经过点A,交AB于点F,与BC相切于点E.点D为BC的中点,连结AD、OE、AE.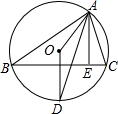 如图,O是△ABC的外心,D是圆上一点,且OD⊥BC,AE是BC边上的高.试探索∠OAD与∠EAD的大小关系,并说明理由.
如图,O是△ABC的外心,D是圆上一点,且OD⊥BC,AE是BC边上的高.试探索∠OAD与∠EAD的大小关系,并说明理由.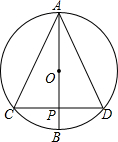 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是
如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是