题目内容
阅读下面的材料:
1×2=
(1×2×3-0×1×2),
2×3=
(2×3×4-1×2×3),
3×4=
(3×4×5-2×3×4)
由以上三个等式相加可得
1×2+2×3+3×4=
×3×4×5=20
根据以上材料,请你计算下列各题:
(1)1×2+2×3+3×4+…+10×11(写出过程);
(2)1×2+2×3+3×4+…+n(n+1)=
(3)模仿上面的材料,试计算1×2×3+2×3×4+3×4×5+…+10×11×12的结果(写过程)
1×2=
| 1 |
| 3 |
2×3=
| 1 |
| 3 |
3×4=
| 1 |
| 3 |
由以上三个等式相加可得
1×2+2×3+3×4=
| 1 |
| 3 |
根据以上材料,请你计算下列各题:
(1)1×2+2×3+3×4+…+10×11(写出过程);
(2)1×2+2×3+3×4+…+n(n+1)=
(3)模仿上面的材料,试计算1×2×3+2×3×4+3×4×5+…+10×11×12的结果(写过程)
考点:规律型:数字的变化类
专题:阅读型
分析:(1)利用已知材料得出原式=
×10×11×12,进而求出即可;
(2)利用(1)中所求,进而求出即可;
(3)仿照已知得出原式=
(1×2×3×4)+
(2×3×4×5-1×2×3×4)+
(3×4×5×6-2×3×4×5)+…+
(10×11×12×13-9×10×11×12)
进而求出即可.
| 1 |
| 3 |
(2)利用(1)中所求,进而求出即可;
(3)仿照已知得出原式=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
进而求出即可.
解答:解:(1)1×2+2×3+3×4+…+10×11
=
(1×2×3-0×1×2)+
(2×3×4-1×2×3)+
(3×4×5-2×3×4)+…+
(10×11×12-9×10×11)
=
(1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+10×11×12-9×10×11)
=
×10×11×12
=440;
(2)1×2+2×3+3×4+…+n(n+1)
=
(1×2×3-0×1×2)+
(2×3×4-1×2×3)+
(3×4×5-2×3×4)+…+
[n×(n+1)×(n+2)-(n-1)×n×(n+1)]
=
n×(n+1)×(n+2);
(3)1×2×3+2×3×4+3×4×5+…+10×11×12
=
(1×2×3×4)+
(2×3×4×5-1×2×3×4)+
(3×4×5×6-2×3×4×5)+…+
(10×11×12×13-9×10×11×12)
=
×10×11×12×13
=4290.
=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
=
| 1 |
| 3 |
=440;
(2)1×2+2×3+3×4+…+n(n+1)
=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
(3)1×2×3+2×3×4+3×4×5+…+10×11×12
=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
=
| 1 |
| 4 |
=4290.
点评:此题主要考查了数字变化规律,根据题意得出正确变化规律是解题关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
四个数-5,0,
,
中为无理数的是( )
| 1 |
| 2 |
| 3 |
| A、-5 | ||
| B、0 | ||
C、
| ||
D、
|
 下面左图所示的几何体的俯视图是( )
下面左图所示的几何体的俯视图是( )A、 |
B、 |
C、 |
D、 |
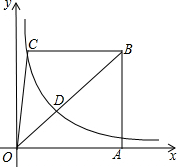 如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线y=
如图,已知梯形ABCO的底边AO在x轴上,BC∥AO,AB⊥AO,过点C的双曲线y=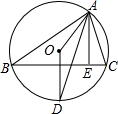 如图,O是△ABC的外心,D是圆上一点,且OD⊥BC,AE是BC边上的高.试探索∠OAD与∠EAD的大小关系,并说明理由.
如图,O是△ABC的外心,D是圆上一点,且OD⊥BC,AE是BC边上的高.试探索∠OAD与∠EAD的大小关系,并说明理由. 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为