��Ŀ����
4�� ��ͼ����A��BΪx���ϵ����㣬��C��DΪy���ϵ����㣬����A��C��B��������C1��һ�����뾭����A��D��B��������C2��һ������ϳ�һ��������ߣ����ǰ�����������߳�Ϊ�����ߡ�����֪��C������Ϊ��0��3������M��������C2��y=mx2-4mx-12m��m��0���Ķ��㣮
��ͼ����A��BΪx���ϵ����㣬��C��DΪy���ϵ����㣬����A��C��B��������C1��һ�����뾭����A��D��B��������C2��һ������ϳ�һ��������ߣ����ǰ�����������߳�Ϊ�����ߡ�����֪��C������Ϊ��0��3������M��������C2��y=mx2-4mx-12m��m��0���Ķ��㣮��1����A��B��������ꣻ
��2���ڵ�һ�����ڵ�������C1���Ƿ����һ��P��ʹ�á�PBC�������������ڣ������PBC��������ֵ���������ڣ���˵�����ɣ�
��3������AC��CM��DA����AC��DMʱ��֤����AD��CM��
���� ��1����y=0����y=mx2-4mx-12m���������A��B��������ꣻ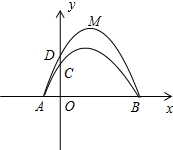
��2�����õ�A��B��C�����꼴�����������C1�Ľ���ʽ�������ֱ��BC�Ľ���ʽ��Ȼ����P�ĺ�����Ϊa������P��PE��x���ڵ�E����ֱ��BC�ڵ�F�����ԡ�PBC�����Ϊ$\frac{1}{2}$PF•OB���г���PBC�������a�ĺ�����ϵʽ�����ö��κ��������ʼ��������PBC��������ֵ��
��3����AC��DMʱ��AD��CM����֤���ı���ACMDʱƽ���ı��Σ�����ֻ��Ҫ֤��AC=DM���ɣ�����ֱ��AC��DM�Ľ���ʽ�����m��ֵ�����ɹ��ɶ�����֤AC=DM���ɣ�
��� �⣺��1����y=0����y=mx2-4mx-12m��
��0=mx2-4mx-12m��
��x=-2��x=6��
��A��-2��0����B��6��0����
��2����������C1�Ľ���ʽΪy=a��x+2����x-6����
��C��0��3������y=a��x+2����x-6����
��3=-12a��
��a=-$\frac{1}{4}$��
�������ߵĽ���ʽΪy=-$\frac{1}{4}$��x+2����x-6��=-$\frac{1}{4}$x2+x+3��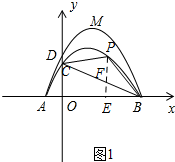
��ֱ��BC�Ľ���ʽΪy=kx+b��
��B��6��0����C��0��3������y=kx+b��
��$\left\{\begin{array}{l}{0=6k+b}\\{3=b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=-$\frac{1}{2}$x+3��
��P��������a��-$\frac{1}{4}$a2+a+3��������0��a��6��
����P��PE��x���ڵ�E����BC�ڵ�F����ͼ1��
��x=a����y=-$\frac{1}{2}$x+3��
��y=-$\frac{1}{2}$a+3��
��F��a��-$\frac{1}{2}$a+3����
��PF=��-$\frac{1}{4}$a2+a+3��-��-$\frac{1}{2}$a+3��
=-$\frac{1}{4}$a2+$\frac{3}{2}$a��
���PBC�����Ϊ��$\frac{1}{2}$PF•OE+$\frac{1}{2}$PF•BE
=$\frac{1}{2}$PF��OE+BE��
=$\frac{1}{2}$PF•OB
=-$\frac{3}{4}$a2+$\frac{9}{2}$a
=-$\frac{3}{4}$��a-3��2+$\frac{27}{4}$��
��a=3ʱ����PBC��������ֵΪ$\frac{27}{4}$��
��3����ͼ2���ɣ�1����֪��A��-2��0����C��0��3����
���ɹ��ɶ�����֪��AC=$\sqrt{13}$��
��ֱ��AC�Ľ���ʽΪy=k1x+b1��
��A��-2��0����C��0��3������y=k1x+b1��
$\left\{\begin{array}{l}{0=-2{k}_{1+}{b}_{1}}\\{3={b}_{1}}\end{array}\right.$��
��$\left\{\begin{array}{l}{{k}_{1}=\frac{3}{2}}\\{{b}_{1}=3}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=$\frac{3}{2}$x+3��
����x=0����y=mx2-4mx-12m��
��y=-12m��
��D��0��-12m����
��������C2�Ľ���ʽ��֪��M��2��-16m����
��ֱ��DM�Ľ���ʽΪy=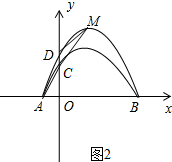 k2x+b2��
k2x+b2��
��AC��DM��
��k2=k1=$\frac{3}{2}$��
��D��0��-12m������y=$\frac{3}{2}$x+b2��
��b2=-12m��
��ֱ��DM�Ľ���ʽΪy=$\frac{3}{2}$x-12m��
��-16m=3-12m��
��m=-$\frac{3}{4}$��
��D��0��9����M��2��12����
���ɹ��ɶ�������DM=$\sqrt{��2-0��^{2}+��12-9��^{2}}$=$\sqrt{13}$��
��AC=DM��
���ı���ACMDʱƽ���ı��Σ�
��AD��CM��
���� ���⿼����κ������ۺ����⣬�漰���κ�������ֵ������ϵ���������ʽ�����ɶ�����֪ʶ���ۺϳ̶Ƚϸߣ�����ѧ���������֪ʶ��������

| ���ϵ��� | 1 | 2 | 3 | 4 | 5 | 6 |
| ���ִ��� | 10 | 15 | 20 | 25 | 20 | 10 |
��2��С��˵��������ʵ�飬һ��ʵ���г���4�㳯�ϵĸ�����$\frac{1}{4}$����С������һ˵����ȷ��Ϊʲô��
��3��С��˵��������ʵ�飬�����1000�Σ���ô����5�㳯�ϵĴ�����200�Σ���С������һ˵����ȷ��Ϊʲô��
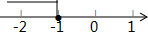 ����x�IJ���ʽ2x+a��-3�Ľ⼯��ͼ��ʾ����a��ȡֵ�ǣ�������
����x�IJ���ʽ2x+a��-3�Ľ⼯��ͼ��ʾ����a��ȡֵ�ǣ�������| A�� | 0 | B�� | -1 | C�� | -2 | D�� | -3 |
| A�� | ֱ�������� | B�� | �۽� | C�� | �߶� | D�� | Բ |




 ��һ���������εĹ����Ŷ����Ŷ���ˮ������߶�Ϊ4m�����Ϊ10m���ֽ�����ͼ�η�����ͼ��ʾ��ֱ������ϵ�У������������ߵĽ���ʽ��
��һ���������εĹ����Ŷ����Ŷ���ˮ������߶�Ϊ4m�����Ϊ10m���ֽ�����ͼ�η�����ͼ��ʾ��ֱ������ϵ�У������������ߵĽ���ʽ�� ij������������Ϊ���˽Ȿ�ؾ��꼶ѧ��ÿ�ܡ��������������ʱ���������������˱��ز��־��꼶ѧ�������ռ��������ݽ����������Ƴ�����������ͳ֭ͼ��ѧ�����������������ʱ��x��h����Ϊ����ȼ���A��x��4����B��4��x��6����C��6��x��8����D��8��x��l0����E��x��10����
ij������������Ϊ���˽Ȿ�ؾ��꼶ѧ��ÿ�ܡ��������������ʱ���������������˱��ز��־��꼶ѧ�������ռ��������ݽ����������Ƴ�����������ͳ֭ͼ��ѧ�����������������ʱ��x��h����Ϊ����ȼ���A��x��4����B��4��x��6����C��6��x��8����D��8��x��l0����E��x��10����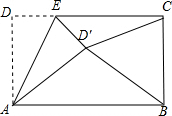 ��ͼ������ABCD�У�AD=5��AB=8����EΪDC��һ�����㣬�ѡ�ADE��AE�۵�������D�Ķ�Ӧ��D�䣬����D��B��D��C�����½����У�
��ͼ������ABCD�У�AD=5��AB=8����EΪDC��һ�����㣬�ѡ�ADE��AE�۵�������D�Ķ�Ӧ��D�䣬����D��B��D��C�����½����У�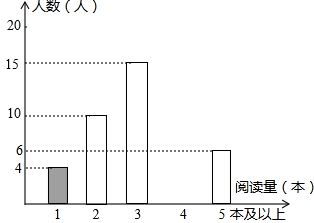 ijѧУΪ�˽�ѧ���Ŀ����Ķ����������ʦ�����鲿��ѧ��������������ڼ�Ŀ����Ķ�������ͳ�Ʒ��������Ƴ���ͼ��ʾ����������ͳ��ͼ����֪����ѧ��������ڼ��Ķ���Ϊ2��������ռ�����������20%��������������Ϣ������������⣺
ijѧУΪ�˽�ѧ���Ŀ����Ķ����������ʦ�����鲿��ѧ��������������ڼ�Ŀ����Ķ�������ͳ�Ʒ��������Ƴ���ͼ��ʾ����������ͳ��ͼ����֪����ѧ��������ڼ��Ķ���Ϊ2��������ռ�����������20%��������������Ϣ������������⣺