题目内容
9.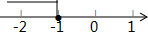 关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )
关于x的不等式2x+a≤-3的解集如图所示,则a的取值是( )| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
分析 将a看作常数求得该不等式解集,再由不等式解集在数轴上的表示可得关于a的方程,解方程即可得a的值.
解答 解:移项,得:2x≤-3-a,
系数化为1,得:x≤$\frac{-3-a}{2}$,
由不等式可知该不等式的解集为x≤-1,
∴$\frac{-3-a}{2}$=-1,
解得:a=-1,
故选:B.
点评 本题主要考查解一元一次不等式与一元一次方程的能力,根据不等式解集在数轴上的表示得出关于a的方程是解题的关键.

练习册系列答案
相关题目
19.化简$\frac{16-{a}^{2}}{{a}^{2}+4a+4}$÷$\frac{a-4}{2a+4}$•$\frac{a-2}{a+4}$,其结果是( )
| A. | -2 | B. | 2 | C. | -$\frac{2(a-2)}{a+2}$ | D. | $\frac{2}{(a+2)^{2}}$ |
14.能够判定一个四边形是菱形的条件是( )
| A. | 对角线互相垂直平分 | B. | 对角线互相平分且相等 | ||
| C. | 对角线相等且互相垂直 | D. | 对角线互相垂直 |
1. 如图,下列条件中,能判定DE∥AC的是( )
如图,下列条件中,能判定DE∥AC的是( )
 如图,下列条件中,能判定DE∥AC的是( )
如图,下列条件中,能判定DE∥AC的是( )| A. | ∠BED=∠EFC | B. | ∠1=∠2 | C. | ∠BEF+∠B=180° | D. | ∠3=∠4 |
19.已知矩形的较短边长为6,对角线相交成60°角,则这个矩形的较长边的长是( )
| A. | 3$\sqrt{6}$ | B. | 6$\sqrt{3}$ | C. | 9 | D. | 12 |
 如图,点A、B为x轴上的两点,点C、D为y轴上的两点,经过A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线成为“月线”.已知点C的坐标为(0,3),点M是抛物线C2:y=mx2-4mx-12m(m<0)的顶点.
如图,点A、B为x轴上的两点,点C、D为y轴上的两点,经过A、C、B的抛物线C1的一部分与经过点A、D、B的抛物线C2的一部分组合成一条封闭曲线,我们把这条封闭曲线成为“月线”.已知点C的坐标为(0,3),点M是抛物线C2:y=mx2-4mx-12m(m<0)的顶点.