题目内容
x取哪些整数值时,不等式5x+2>3(x-1)与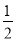 x≤2-
x≤2-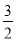 x都成立?
x都成立?
 x取-2,-1,0,1
【解析】【试题分析】
【试题解析】解不等式5x+2>3(x-1)得:得x>-2.5;
解不等式x≤2-x得,x≤1.则这两个不等式解集的公共部分为 ,
因为x取整数,则x取-2,-1,0,1.
故答案为:x取-2,-1,0,1
x取-2,-1,0,1
【解析】【试题分析】
【试题解析】解不等式5x+2>3(x-1)得:得x>-2.5;
解不等式x≤2-x得,x≤1.则这两个不等式解集的公共部分为 ,
因为x取整数,则x取-2,-1,0,1.
故答案为:x取-2,-1,0,1
袋中有红球4个,白球若干个,它们只有颜色上的区别,从袋中随机地取出一个球,如果取得白球的可能性较大,那么袋中白球可能有( )
A. 3个 B. 不足3个
C. 4个 D. 5个或5个以上
 D
【解析】根据取到白球的可能性较大可以判断出白球的数量大于红球的数量,从而得解.
【解析】
∵袋中有红球4个,取到白球的可能性较大,
∴袋中的白球数量大于红球数量,
即袋中白球的个数可能是5个或5个以上.
故选D.
D
【解析】根据取到白球的可能性较大可以判断出白球的数量大于红球的数量,从而得解.
【解析】
∵袋中有红球4个,取到白球的可能性较大,
∴袋中的白球数量大于红球数量,
即袋中白球的个数可能是5个或5个以上.
故选D. 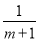 与
与 的最简公分母是__________
的最简公分母是__________
 【解析】试题分析:m2-1=(m+1)(m-1),
所以最简公分母是m2-1.
故答案为:m2-1.
【解析】试题分析:m2-1=(m+1)(m-1),
所以最简公分母是m2-1.
故答案为:m2-1. 某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过105700元购进40台电脑,其中A型电脑每台进价2500元,B型电脑每台进价2800元,A型每台售价3000元,B型每台售价3200元,预计销售额不低于123200元.设A型电脑购进x台、商场的总利润为y(元).
(1)请你设计出进货方案;
(2)求出总利润y(元)与购进A型电脑x(台)的函数关系式,并利用关系式说明哪种方案的利润最大,最大利润是多少元?
(3)商场准备拿出(2)中的最大利润的一部分再次购进A型和B型电脑至少各两台,另一部分为地震灾区购买单价为500元的帐篷若干顶.在钱用尽三样都购买的前提下请直接写出购买A型电脑、B型电脑和帐篷的方案.
 【解析】
(1)设A型电脑购进x台,则B型电脑购进(40﹣x)台,由题意,得
,解得:21≤x≤24。
∵x为整数,∴x=21,22,23,24。
∴有4种购买方案:
方案1:购A型电脑21台,B型电脑19台;
方案2:购A型电脑22台,B型电脑18台;
方案3:购A型电脑23台,B型电脑17台;
方案4:购A型电脑24台,B型电脑16台。
(2)...
【解析】
(1)设A型电脑购进x台,则B型电脑购进(40﹣x)台,由题意,得
,解得:21≤x≤24。
∵x为整数,∴x=21,22,23,24。
∴有4种购买方案:
方案1:购A型电脑21台,B型电脑19台;
方案2:购A型电脑22台,B型电脑18台;
方案3:购A型电脑23台,B型电脑17台;
方案4:购A型电脑24台,B型电脑16台。
(2)... 有一个两位数,其个位数字比十位数字大2,已知这个两位数大于20且小于40,那么这个两位数是__.
 24或35
【解析】【解析】
设这个两位数十位数字为x,则个位数字为x+2,那么这个两位数为10x+x+2.根据题意得:
,解得: .
∵x为正整数,∴x为2或3,
∴10x+x+2=24或35,
则这个两位数是24或35.
故答案为:24或35.
24或35
【解析】【解析】
设这个两位数十位数字为x,则个位数字为x+2,那么这个两位数为10x+x+2.根据题意得:
,解得: .
∵x为正整数,∴x为2或3,
∴10x+x+2=24或35,
则这个两位数是24或35.
故答案为:24或35. 按要求解答下列各题:
(1)解不等式:3x-5<2(2+3x);
(2)解不等式:2x-3≤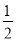 (x+2);
(x+2);
(3)解不等式:  <x-1,并将解集在数轴上表示出来.
<x-1,并将解集在数轴上表示出来.
 (1)x>-3 (2)x≤ (3)x>2,画数轴略
【解析】【试题分析】(1)去括号得: 移项得: 合并同类项得: 系数化为1得:x>-3 ;
(2) 去括号得: 移项得: 合并同类项得: 系数化为1得: x≤ ;
(3)去分母得: 移项得: ,合并得: 系数化为1得:x>2,数轴见解析.
【试题解析】
去括号得:
移项得:
合并同类项得:
系数化为...
(1)x>-3 (2)x≤ (3)x>2,画数轴略
【解析】【试题分析】(1)去括号得: 移项得: 合并同类项得: 系数化为1得:x>-3 ;
(2) 去括号得: 移项得: 合并同类项得: 系数化为1得: x≤ ;
(3)去分母得: 移项得: ,合并得: 系数化为1得:x>2,数轴见解析.
【试题解析】
去括号得:
移项得:
合并同类项得:
系数化为... 如图,在△ABC和△DEC中,∠ABC=∠DEC=90°,连接AD交射线EB于F,AC∥DE,延长CA交射线EB于点G,点F恰好是AD中点。
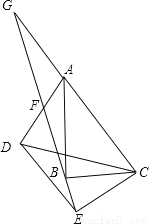
(1)求证:△AFG≌△DFE;
(2)若BC=CE,
①求证:∠ABF=∠DEF;
②若∠BAC=30°,试求∠AFG的度数。
 (1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△A...
(1)证明见解析(2)①证明见解析②∠AFG=60°。
【解析】试题分析:
(1)由AG∥DE易得:∠G=∠DEF;由F是AD的中点易得AF=DF,结合∠AFG=∠DFE,即可证得:△AGF≌△DEF;
(2)①由BC=CE可得∠CBE=∠CEB,结合∠ABC=DEC=90°,易得∠ABF+∠CBE=90°,∠CEB+∠DEF=90°,从而可得∠ABF=∠DEF;
②由△A... 有3人携带会议材料乘坐电梯,这三人的体重共210 kg,每捆材料重20 kg,电梯最大负荷为1 050 kg,则该电梯在此3人乘坐的情况下最多还能搭载_______捆材料.
 42
【解析】(1050-210)
42
【解析】(1050-210) 如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
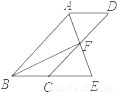
 (1)详见解析;(2).
【解析】试题分析:(1)由平行四边形的性质和角平分线易证∠BAE=∠BEA,根据等腰三角形的性质可得AB=BE;(2)易证△ABE是等边三角形,根据等边三角形的性质可得AE=AB=4,AF=EF=2,由勾股定理求出BF,再由AAS证明△ADF≌△ECF,即△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积=AE•BF,即可得出结果.
...
(1)详见解析;(2).
【解析】试题分析:(1)由平行四边形的性质和角平分线易证∠BAE=∠BEA,根据等腰三角形的性质可得AB=BE;(2)易证△ABE是等边三角形,根据等边三角形的性质可得AE=AB=4,AF=EF=2,由勾股定理求出BF,再由AAS证明△ADF≌△ECF,即△ADF的面积=△ECF的面积,因此平行四边形ABCD的面积=△ABE的面积=AE•BF,即可得出结果.
... 
