题目内容
有一个两位数,其个位数字比十位数字大2,已知这个两位数大于20且小于40,那么这个两位数是__.
 24或35
【解析】【解析】
设这个两位数十位数字为x,则个位数字为x+2,那么这个两位数为10x+x+2.根据题意得:
,解得: .
∵x为正整数,∴x为2或3,
∴10x+x+2=24或35,
则这个两位数是24或35.
故答案为:24或35.
24或35
【解析】【解析】
设这个两位数十位数字为x,则个位数字为x+2,那么这个两位数为10x+x+2.根据题意得:
,解得: .
∵x为正整数,∴x为2或3,
∴10x+x+2=24或35,
则这个两位数是24或35.
故答案为:24或35.
把下列事件划分为两类,并说出划分标准.
①向空中抛一块石头,石头会飞向太空;
②甲、乙两名同学进行羽毛球比赛,甲获胜;
③从一副扑克牌中随意抽取一张牌,这张牌正好是红桃;
④黑暗中从一大串钥匙中随意选中一把,并用它打开了大门;
⑤两个负数的商小于0;
⑥在你们班中,任意选出一名同学,该同学是男生;
⑦明天的太阳从西方升起.
 答案见解析
【解析】试题分析:按事件名称可将给出的几个事件划分为不可能事件和随机事件;然后按照事件发生的确定性,可将事件分为确定事件和不确定事件,据此进行分类即可.
解:按事件名称划分:不可能事件:①⑤⑦;随机事件:②③④⑥.
答案见解析
【解析】试题分析:按事件名称可将给出的几个事件划分为不可能事件和随机事件;然后按照事件发生的确定性,可将事件分为确定事件和不确定事件,据此进行分类即可.
解:按事件名称划分:不可能事件:①⑤⑦;随机事件:②③④⑥. 先化简,后求值: 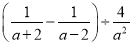 ,其中
,其中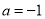
 【解析】试题分析:先将括号内的分式通分相减,然后将除法转化为乘法,约分化成最简后代入字母的值计算即可.
试题解析:
【解析】
原式=
=
=,
当a=-1时,
原式=
=.
【解析】试题分析:先将括号内的分式通分相减,然后将除法转化为乘法,约分化成最简后代入字母的值计算即可.
试题解析:
【解析】
原式=
=
=,
当a=-1时,
原式=
=. 计算 的结果是( )
的结果是( )
A. 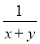 B.
B. 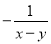 C.
C. 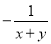 D.
D. 
 D
【解析】试题分析:原式=
=
=
=.
故选D.
D
【解析】试题分析:原式=
=
=
=.
故选D. 某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖纸盒.

(1)现有正方形纸板162张,长方形纸板340张.若要做两种纸盒共100个,设做竖式纸盒x个.
①根据题意,完成以下表格:
纸盒 纸板 | 竖式纸盒(个) | 横式纸盒(个) |
x | 100﹣x | |
正方形纸板(张) | 2(100﹣x) | |
长方形纸板(张) | 4x |
②按两种纸盒的生产个数来分,有哪几种生产方案?
(2)若有正方形纸162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<306.求a的值.
 (1)①见解析;②有三种方案:生产竖式纸盒38个,横式纸盒62个;生产竖式纸盒39个,横式纸盒61个;生产竖式纸盒40个,横式纸盒60个;
(2)293或298或303(写出其中一个即可).
【解析】试题分析:(1)①可根据竖式纸盒+横式纸盒=100个,每个竖式纸盒需1个正方形纸板和4个长方形纸板,每个横式纸盒需3个长方形纸板和2个正方形纸板来填空.
②生产竖式纸盒用的正方形纸板...
(1)①见解析;②有三种方案:生产竖式纸盒38个,横式纸盒62个;生产竖式纸盒39个,横式纸盒61个;生产竖式纸盒40个,横式纸盒60个;
(2)293或298或303(写出其中一个即可).
【解析】试题分析:(1)①可根据竖式纸盒+横式纸盒=100个,每个竖式纸盒需1个正方形纸板和4个长方形纸板,每个横式纸盒需3个长方形纸板和2个正方形纸板来填空.
②生产竖式纸盒用的正方形纸板... x取哪些整数值时,不等式5x+2>3(x-1)与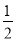 x≤2-
x≤2-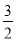 x都成立?
x都成立?
 x取-2,-1,0,1
【解析】【试题分析】
【试题解析】解不等式5x+2>3(x-1)得:得x>-2.5;
解不等式x≤2-x得,x≤1.则这两个不等式解集的公共部分为 ,
因为x取整数,则x取-2,-1,0,1.
故答案为:x取-2,-1,0,1
x取-2,-1,0,1
【解析】【试题分析】
【试题解析】解不等式5x+2>3(x-1)得:得x>-2.5;
解不等式x≤2-x得,x≤1.则这两个不等式解集的公共部分为 ,
因为x取整数,则x取-2,-1,0,1.
故答案为:x取-2,-1,0,1 不等式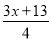 >
>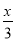 +2的解是_________.
+2的解是_________.
 x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3.
x>-3
【解析】>+2, 去分母得: 去括号得: 移项及合并得: 系数化为1得: .
故答案为x>-3. 小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a>8),就站在A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人.
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少?(用含a的代数式表示)
(2)此时,若小杰迅速从A窗口队伍转移到B窗口后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围.(不考虑其它因素)
 (1)分;(2)a>20
【解析】
试题分析:(1)根据“过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍”即可列出代数式;
(2)根据“到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少”即可列不等式求解.
(1)由题意得他继续在A窗口排队到达窗口所花的时间为分;
(2)由题意得,解得a>20.
(1)分;(2)a>20
【解析】
试题分析:(1)根据“过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍”即可列出代数式;
(2)根据“到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少”即可列不等式求解.
(1)由题意得他继续在A窗口排队到达窗口所花的时间为分;
(2)由题意得,解得a>20. 我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
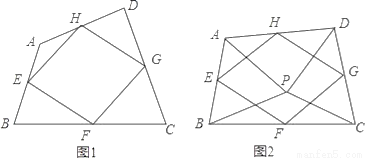
 (1)证明见解析;(2)四边形EFGH是菱形,证明见解析;(3)四边形EFGH是正方形.
【解析】试题分析:(1)如图1中,连接BD,根据三角形中位线定理只要证明EH∥FG,EH=FG即可.
(2)四边形EFGH是菱形.先证明△APC≌△BPD,得到AC=BD,再证明EF=FG即可.
(3)四边形EFGH是正方形,只要证明∠EHG=90°,利用△APC≌△BPD,得∠ACP=∠B...
(1)证明见解析;(2)四边形EFGH是菱形,证明见解析;(3)四边形EFGH是正方形.
【解析】试题分析:(1)如图1中,连接BD,根据三角形中位线定理只要证明EH∥FG,EH=FG即可.
(2)四边形EFGH是菱形.先证明△APC≌△BPD,得到AC=BD,再证明EF=FG即可.
(3)四边形EFGH是正方形,只要证明∠EHG=90°,利用△APC≌△BPD,得∠ACP=∠B... 
