��Ŀ����
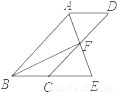
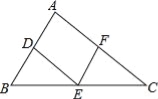
��ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AE��CD�ڵ�F����BC���ӳ����ڵ�E��
��1����֤��BE=CD��
��2������BF����BF��AE����BEA=60�㣬AB=4����ƽ���ı���ABCD�������
 ��1�������������2��.
�������������������1����ƽ���ı��ε����ʺͽ�ƽ������֤��BAE=��BEA�����ݵ��������ε����ʿɵ�AB=BE����2����֤��ABE�ǵȱ������Σ����ݵȱ������ε����ʿɵ�AE=AB=4��AF=EF=2���ɹ��ɶ������BF������AAS֤����ADF�ա�ECF������ADF�����=��ECF����������ƽ���ı���ABCD�����=��ABE�����=AE•BF�����ɵó������
...
��1�������������2��.
�������������������1����ƽ���ı��ε����ʺͽ�ƽ������֤��BAE=��BEA�����ݵ��������ε����ʿɵ�AB=BE����2����֤��ABE�ǵȱ������Σ����ݵȱ������ε����ʿɵ�AE=AB=4��AF=EF=2���ɹ��ɶ������BF������AAS֤����ADF�ա�ECF������ADF�����=��ECF����������ƽ���ı���ABCD�����=��ABE�����=AE•BF�����ɵó������
...
 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�xȡ��Щ����ֵʱ������ʽ5x��2��3(x��1)��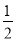 x��2��
x��2��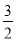 x��������
x��������
 xȡ��2����1,0,1
�������������������
������������ⲻ��ʽ5x��2��3(x��1)�ã���x����2.5��
�ⲻ��ʽx��2��x�ã�x��1.������������ʽ�⼯�Ĺ�������Ϊ ��
��Ϊxȡ��������xȡ��2����1,0,1.
�ʴ�Ϊ��xȡ��2����1,0,1
xȡ��2����1,0,1
�������������������
������������ⲻ��ʽ5x��2��3(x��1)�ã���x����2.5��
�ⲻ��ʽx��2��x�ã�x��1.������������ʽ�⼯�Ĺ�������Ϊ ��
��Ϊxȡ��������xȡ��2����1,0,1.
�ʴ�Ϊ��xȡ��2����1,0,1 ��֪����ʽ��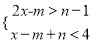 �Ľ⼯Ϊ��1��x��1����m+n��2014��ֵ���ڶ��٣�
�Ľ⼯Ϊ��1��x��1����m+n��2014��ֵ���ڶ��٣�
 1
��������������������ⲻ��ʽ�ⲻ��ʽ2x��m��n��1��x�����ɲ���ʽ��Ľ⼯Ϊ��1��x��1�ɵ�=��1���Ӷ�֪m+n��ֵ�����뼴�ɣ�
�����������
�ⲻ��ʽ2x��m��n��1���ã�x����
�߲���ʽ��Ľ⼯Ϊ��1��x��1��
��=��1��
��m+n=��1��
��m+n��2014=����1��2014=1��
1
��������������������ⲻ��ʽ�ⲻ��ʽ2x��m��n��1��x�����ɲ���ʽ��Ľ⼯Ϊ��1��x��1�ɵ�=��1���Ӷ�֪m+n��ֵ�����뼴�ɣ�
�����������
�ⲻ��ʽ2x��m��n��1���ã�x����
�߲���ʽ��Ľ⼯Ϊ��1��x��1��
��=��1��
��m+n=��1��
��m+n��2014=����1��2014=1�� ����ʽ��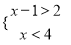 �Ľ⼯�ǣ�������
�Ľ⼯�ǣ�������
A. x��3 B. 3��x��4 C. x��4 D. ��
 B
���������ⲻ��ʽx��1��2���ã�x��3��
���ʽ��Ľ⼯Ϊ��3��x��4��
��ѡ��B��
B
���������ⲻ��ʽx��1��2���ã�x��3��
���ʽ��Ľ⼯Ϊ��3��x��4��
��ѡ��B�� ���Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��֤���е��ı���EFGH��ƽ���ı��Σ�
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90�㣬�����������䣬ֱ��д���е��ı���EFGH����״��������֤����
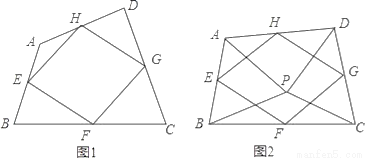
 ��1��֤������������2���ı���EFGH�����Σ�֤������������3���ı���EFGH��������.
�������������������1����ͼ1�У�����BD��������������λ�߶���ֻҪ֤��EH��FG��EH=FG���ɣ�
��2���ı���EFGH�����Σ���֤����APC�ա�BPD���õ�AC=BD����֤��EF=FG���ɣ�
��3���ı���EFGH�������Σ�ֻҪ֤����EHG=90�㣬���á�APC�ա�BPD���á�ACP=��B...
��1��֤������������2���ı���EFGH�����Σ�֤������������3���ı���EFGH��������.
�������������������1����ͼ1�У�����BD��������������λ�߶���ֻҪ֤��EH��FG��EH=FG���ɣ�
��2���ı���EFGH�����Σ���֤����APC�ա�BPD���õ�AC=BD����֤��EF=FG���ɣ�
��3���ı���EFGH�������Σ�ֻҪ֤����EHG=90�㣬���á�APC�ա�BPD���á�ACP=��B... ��ͼ������һ�������Σ��ֱ�������������������е�õ�ͼ�ڣ�������ͼ���м�С���������ߵ��е�õ�ͼ�ۣ��������ķ���������ȥ����n��ͼ���й��������εĸ���Ϊ__��
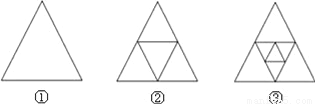
 4n��3
������������������ڢ���1�������Σ�1=4��1-3��
�ڢ���5�������Σ�5=4��2-3��
�ڢ���9�������Σ�9=4��3-3��
���n��ͼ���й��������εĸ�����4n-3
4n��3
������������������ڢ���1�������Σ�1=4��1-3��
�ڢ���5�������Σ�5=4��2-3��
�ڢ���9�������Σ�9=4��3-3��
���n��ͼ���й��������εĸ�����4n-3 ��ͼ����?ABCD�ضԽ���AC�۵���ʹ��B����B�䴦������1=��2=44�㣬���BΪ��������
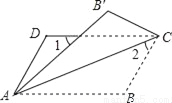
A. 66�� B. 104�� C. 114�� D. 124��
 C
��������������������ı���ABCD��ƽ���ı��Σ�
��AB��CD��
���ACD=��BAC��
���۵������ʵã���BAC=��B��AC��
���BAC=��ACD=��B��AC=
���B=180��-��2-��BAC=180��-44��-22��=114�㣻
��ѡC��
C
��������������������ı���ABCD��ƽ���ı��Σ�
��AB��CD��
���ACD=��BAC��
���۵������ʵã���BAC=��B��AC��
���BAC=��ACD=��B��AC=
���B=180��-��2-��BAC=180��-44��-22��=114�㣻
��ѡC�� ��ͼ���ڡ�ABC�У���D��E��F�ֱ��DZ�AB��BC��CA�ϵ��е㣬��AB=6cm��AC=8cm�����ı���ADEF���ܳ����� cm��
 14.
��������
�����������D��E�ֱ�AB��BC���е㣬��AD=AB��DE=AC.ͬ��AF=AC��EF=AB.��l�ı���ADEF=AD+DE+EF+AF=��AB+AC+AB+AC��=AB+AC=14cm.
14.
��������
�����������D��E�ֱ�AB��BC���е㣬��AD=AB��DE=AC.ͬ��AF=AC��EF=AB.��l�ı���ADEF=AD+DE+EF+AF=��AB+AC+AB+AC��=AB+AC=14cm. С��������һ��ƽ���ı��β����������ͼ���Ŀ飬Ϊ�������̵��䵽һ����ԭ����ͬ��ƽ���ı��β����������������鲣��������Ӧ���ǣ��� ����
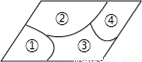
A. �٣��� B. �٣��� C. �ۣ��� D. �ڣ���
 D
�����������������⿼�����ƽ���ı��ε�����.
����������IJ����еĢں͢������ӵģ����Եõ��ı��εĴ�С.
��ѡB.
D
�����������������⿼�����ƽ���ı��ε�����.
����������IJ����еĢں͢������ӵģ����Եõ��ı��εĴ�С.
��ѡB. 
