题目内容
袋中有红球4个,白球若干个,它们只有颜色上的区别,从袋中随机地取出一个球,如果取得白球的可能性较大,那么袋中白球可能有( )
A. 3个 B. 不足3个
C. 4个 D. 5个或5个以上
 D
【解析】根据取到白球的可能性较大可以判断出白球的数量大于红球的数量,从而得解.
【解析】
∵袋中有红球4个,取到白球的可能性较大,
∴袋中的白球数量大于红球数量,
即袋中白球的个数可能是5个或5个以上.
故选D.
D
【解析】根据取到白球的可能性较大可以判断出白球的数量大于红球的数量,从而得解.
【解析】
∵袋中有红球4个,取到白球的可能性较大,
∴袋中的白球数量大于红球数量,
即袋中白球的个数可能是5个或5个以上.
故选D.
如图,△ABC和△A′B′C′关于直线l对称,下列结论中:
①△ABC≌△A′B′C′;
②∠BAC′=∠B′AC;
③l垂直平分CC′;
④直线BC和B′C′的交点不一定在l上,
正确的有( )
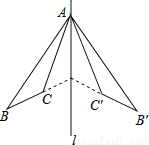
A. 4个 B. 3个 C. 2个 D. 1个
 B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称,
∴①△ABC≌△A′B′C′,正确;
②∠BAC=∠B′AC′,
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′,
即∠BAC′=∠B′AC正确;
③l垂直平分CC′,正确;
④应为:直线BC和B′C′的交点一定在l上,故本小题错误.
综上所述,结论正确的是①②③共3个.
故...
B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称,
∴①△ABC≌△A′B′C′,正确;
②∠BAC=∠B′AC′,
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′,
即∠BAC′=∠B′AC正确;
③l垂直平分CC′,正确;
④应为:直线BC和B′C′的交点一定在l上,故本小题错误.
综上所述,结论正确的是①②③共3个.
故... 嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
 (1)见解析;(2)见解析
【解析】试题分析:(1)命题的题设为“两组对边分别相等的四边形”,结论是“是平行四边形”,即可得到结论;
(2)连接BD,利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC,∠ABD=∠CDB,进而可得AB∥CD,AD∥CB,根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形;
(3)把命题“两组对边分别相等的四边形是平行四...
(1)见解析;(2)见解析
【解析】试题分析:(1)命题的题设为“两组对边分别相等的四边形”,结论是“是平行四边形”,即可得到结论;
(2)连接BD,利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC,∠ABD=∠CDB,进而可得AB∥CD,AD∥CB,根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形;
(3)把命题“两组对边分别相等的四边形是平行四... 已知四边形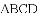
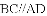
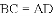
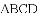
A. 6种 B. 5种 C. 4种 D. 3种
 C
【解析】平行四边形的判定,平行四边形的判定方法共有五种,在四边形中如果有:
1、四边形的两组对边分别平行;
2、一组对边平行且相等;
3、两组对边分别相等;
4、对角线互相平分;
5、两组对角分别相等.则四边形是平行四边形
根据平行四边形的判定,符合条件的有4种,分别是:①②、③④、②③、①④.
故选C
C
【解析】平行四边形的判定,平行四边形的判定方法共有五种,在四边形中如果有:
1、四边形的两组对边分别平行;
2、一组对边平行且相等;
3、两组对边分别相等;
4、对角线互相平分;
5、两组对角分别相等.则四边形是平行四边形
根据平行四边形的判定,符合条件的有4种,分别是:①②、③④、②③、①④.
故选C 把下列事件划分为两类,并说出划分标准.
①向空中抛一块石头,石头会飞向太空;
②甲、乙两名同学进行羽毛球比赛,甲获胜;
③从一副扑克牌中随意抽取一张牌,这张牌正好是红桃;
④黑暗中从一大串钥匙中随意选中一把,并用它打开了大门;
⑤两个负数的商小于0;
⑥在你们班中,任意选出一名同学,该同学是男生;
⑦明天的太阳从西方升起.
 答案见解析
【解析】试题分析:按事件名称可将给出的几个事件划分为不可能事件和随机事件;然后按照事件发生的确定性,可将事件分为确定事件和不确定事件,据此进行分类即可.
解:按事件名称划分:不可能事件:①⑤⑦;随机事件:②③④⑥.
答案见解析
【解析】试题分析:按事件名称可将给出的几个事件划分为不可能事件和随机事件;然后按照事件发生的确定性,可将事件分为确定事件和不确定事件,据此进行分类即可.
解:按事件名称划分:不可能事件:①⑤⑦;随机事件:②③④⑥. 下列事件中,是必然事件的是( )
A. 两条线段可以组成一个三角形
B. 400人中有两个人的生日在同一天
C. 早上的太阳从西方升起
D. 打开电视机,它正在播放动画片
 B
【解析】试题解析:A. 两条线段可以组成一个三角形是不可能事件,故错误;
B.400人中有两个人的生日在同一天是必然事件,故正确;
C. 早上的太阳从西方升起是不可能事件,故错误;
D. 打开电视机,它正在播放动画片是随机事件,故错误;
故选B.
B
【解析】试题解析:A. 两条线段可以组成一个三角形是不可能事件,故错误;
B.400人中有两个人的生日在同一天是必然事件,故正确;
C. 早上的太阳从西方升起是不可能事件,故错误;
D. 打开电视机,它正在播放动画片是随机事件,故错误;
故选B. 计算: 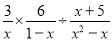 .
.
 【解析】试题分析:根据分式乘除法法则计算即可.
试题解析:原式==.
【解析】试题分析:根据分式乘除法法则计算即可.
试题解析:原式==. 下列分式,对于任意的x值总有意义的是( )
A. 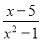 B.
B. 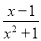 C.
C. 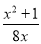 D.
D. 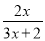
 B
【解析】试题解析:因为分式有意义的条件是分母不能为0,B选项的分母为,
故选B.
B
【解析】试题解析:因为分式有意义的条件是分母不能为0,B选项的分母为,
故选B. x取哪些整数值时,不等式5x+2>3(x-1)与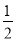 x≤2-
x≤2-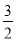 x都成立?
x都成立?
 x取-2,-1,0,1
【解析】【试题分析】
【试题解析】解不等式5x+2>3(x-1)得:得x>-2.5;
解不等式x≤2-x得,x≤1.则这两个不等式解集的公共部分为 ,
因为x取整数,则x取-2,-1,0,1.
故答案为:x取-2,-1,0,1
x取-2,-1,0,1
【解析】【试题分析】
【试题解析】解不等式5x+2>3(x-1)得:得x>-2.5;
解不等式x≤2-x得,x≤1.则这两个不等式解集的公共部分为 ,
因为x取整数,则x取-2,-1,0,1.
故答案为:x取-2,-1,0,1 
