题目内容
14. 如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )
如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于( )| A. | 130° | B. | 120° | C. | 110° | D. | 100° |
分析 先设出∠BOE=α,再表示出∠DOE=α∠AOD=4α,建立方程求出α,最用利用对顶角,角之间的和差即可.
解答 解:设∠BOE=α,
∵∠AOD:∠BOE=4:1,
∴∠AOD=4α,
∵OE平分∠BOD,
∴∠DOE=∠BOE=α
∴∠AOD+∠DOE+∠BOE=180°,
∴4α+α+α=180°,
∴α=30°,
∴∠AOD=4α=120°,
∴∠BOC=∠AOD=120°,
∵OF平分∠COB,
∴∠COF=$\frac{1}{2}$∠BOC=60°,
∵∠AOC=∠BOD=2α=60°,
∴∠AOF=∠AOC+∠COF=120°,
故选B
点评 此题是对顶角,邻补角题,还考查了角平分线的意义,解本题的关键是找到角与角之间的关系,用方程的思想解决几何问题是初中阶段常用的方法.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
9.一个菱形的两条对角线长分别为6cm和10cm,则这个菱形的面积是( )
| A. | 60cm2 | B. | 30cm2 | C. | 32cm2 | D. | 15cm2 |
6.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )
| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
3. 如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
 如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )| A. | 60° | B. | 25° | C. | 35° | D. | 45° |

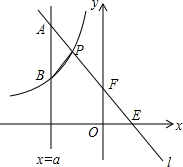 如图,一次函数y=kx+b的图象与坐标轴分别交于点E,F,与双曲线y=-$\frac{4}{x}$(x<0)交于点P(-1,n),且F是PE的中点,直线x=a与直线l交于点A,与双曲线交于点B(不同于A),设线段AB的长度为m,求关于a的函数关系式.
如图,一次函数y=kx+b的图象与坐标轴分别交于点E,F,与双曲线y=-$\frac{4}{x}$(x<0)交于点P(-1,n),且F是PE的中点,直线x=a与直线l交于点A,与双曲线交于点B(不同于A),设线段AB的长度为m,求关于a的函数关系式. 如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长. 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,那么当点R应运动到MQ中点时,△MNR的面积( )
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止,设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,那么当点R应运动到MQ中点时,△MNR的面积( )