题目内容
10. 如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )
如图,直线m∥n,Rt△ABC的顶点A在直线n上,∠C=90°,若∠1=25°,∠2=70°,则∠B=( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
分析 根据两直线平行,内错角相等可得∠3=∠2,再求出∠BAC,然后根据直角三角形两锐角互余列式计算即可得解.
解答  解:∵m∥n,
解:∵m∥n,
∴∠3=∠2=70°,
∴∠BAC=∠3-∠1=70°-25°=45°,
∵∠C=90°,
∴∠B=90°-∠BAC=90°-45°=45°.
故选C.
点评 本题考查了平行线的性质,直角三角形两锐角互余的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
1. 已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
①AG⊥BE;②∠DGE=60°;③BF=2FG;④AD+$\sqrt{2}$DC=AB.
其中正确的结论有( )
 已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:①AG⊥BE;②∠DGE=60°;③BF=2FG;④AD+$\sqrt{2}$DC=AB.
其中正确的结论有( )
| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ②③④ |
18.若方程组$\left\{\begin{array}{l}5x-4y=m\\ 3x+5y=8\end{array}\right.$中x与y互为相反数,则m的值是( )
| A. | 1 | B. | -1 | C. | -36 | D. | 36 |
15.不等式组$\left\{\begin{array}{l}{2x≥x-3}\\{\frac{x+2}{3}>x}\end{array}\right.$的解集为( )
| A. | x≥-3 | B. | x<1 | C. | -3≤x<1 | D. | x>1 |
20.举反例说明“一个锐角的余角小于这个角”是假命题,下面错误的是( )
| A. | 设一个角是45°,它的余角是45°,但45°=45° | |
| B. | 设一个角是60°,它的余角是30°,但30°<60° | |
| C. | 设一个角是30°,它的余角是60°,但60°>30° | |
| D. | 设一个角是10°,它的余角是80°,但80°>10° |

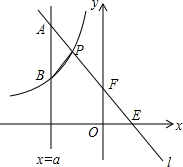 如图,一次函数y=kx+b的图象与坐标轴分别交于点E,F,与双曲线y=-$\frac{4}{x}$(x<0)交于点P(-1,n),且F是PE的中点,直线x=a与直线l交于点A,与双曲线交于点B(不同于A),设线段AB的长度为m,求关于a的函数关系式.
如图,一次函数y=kx+b的图象与坐标轴分别交于点E,F,与双曲线y=-$\frac{4}{x}$(x<0)交于点P(-1,n),且F是PE的中点,直线x=a与直线l交于点A,与双曲线交于点B(不同于A),设线段AB的长度为m,求关于a的函数关系式. 如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.