题目内容
10.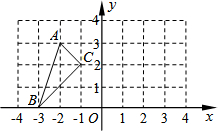 如图,△ABC的顶点都在方格线的交点(格点)上.
如图,△ABC的顶点都在方格线的交点(格点)上.(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是(2,-3).
分析 (1)直接利用旋转的性质得出对应点位置进而得出答案;
(2)直接利用平移的性质得出对应点位置进而得出答案;
(3)利用关于原点对称点的性质直接得出答案.
解答  解:(1)如图所示:△A′B′C′,即为所求;
解:(1)如图所示:△A′B′C′,即为所求;
(2)如图所示:△A″B″C″,即为所求;
(3)将△ABC绕原点O旋转180°,A的对应点A1的坐标是(2,-3).
故答案为:(2,-3).
点评 此题主要考查了旋转变换以及平移变换,根据题意得出对应点位置是解题关键.

练习册系列答案
相关题目
18.把2x2y-8xy+8y分解因式,正确的是( )
| A. | 2(x2y-4xy+4y) | B. | 2y(x2-4x+4) | C. | 2y(x-2)2 | D. | 2y(x+2)2 |
15.在平面直角坐标系中,把点P首先向左平移7个单位,再向上平移5个单位得到点M,作点M关于Y轴的对称点N,已知N的坐标是(5,1),那么P点坐标是( )
| A. | (2,-4) | B. | (6,-4) | C. | (6,-1) | D. | (2,-1) |
1. 已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
①AG⊥BE;②∠DGE=60°;③BF=2FG;④AD+$\sqrt{2}$DC=AB.
其中正确的结论有( )
 已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:
已知,等腰Rt△ABC中AC=BC,点D在BC上,且∠ADB=105°,ED⊥AB,G是AF延长线上一点,BE交AG于F,且DE=2FG,连GE、GB.则下列结论:①AG⊥BE;②∠DGE=60°;③BF=2FG;④AD+$\sqrt{2}$DC=AB.
其中正确的结论有( )
| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ②③④ |
 如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.