题目内容
4.下列命题是真命题的有( )①对顶角相等;②两直线平行,内错角相等;③两个锐角对应相等的两个直角三角形全等;④若a2=b2,则a=b;⑤若a>b,则ac2>bc2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由对顶角的性质、平行线的性质、全等三角形的判定.平方的定义对个选项判断即可.
解答 解:①对顶角相等;①是真命题;
②两直线平行,内错角相等;②是真命题;
③两个锐角对应相等的两个直角三角形不一定全等;③是假命题;
④若a2=b2,则a=b或a=-b;④是假命题;
⑤若a>b,则ac2>bc2.⑤是假命题;
真命题的个数有2个,故选:B.
点评 本题考查了命题与定理、对顶角的性质、平行线的性质、全等三角形的判定等知识;熟记各性质和判定是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.在平面直角坐标系中,把点P首先向左平移7个单位,再向上平移5个单位得到点M,作点M关于Y轴的对称点N,已知N的坐标是(5,1),那么P点坐标是( )
| A. | (2,-4) | B. | (6,-4) | C. | (6,-1) | D. | (2,-1) |
15.不等式组$\left\{\begin{array}{l}{2x≥x-3}\\{\frac{x+2}{3}>x}\end{array}\right.$的解集为( )
| A. | x≥-3 | B. | x<1 | C. | -3≤x<1 | D. | x>1 |
16.下列各组二次根式中,不能合并的是( )
| A. | $\sqrt{20}$和$\sqrt{5}$ | B. | $\sqrt{12}$和$\sqrt{27}$ | C. | $\sqrt{\frac{1}{3}}$或$\sqrt{\frac{2}{3}}$ | D. | $\sqrt{45a}$和$\sqrt{125a}$ |
13.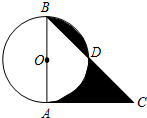 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )
 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )| A. | $\frac{π}{2}$ | B. | 2 | C. | π | D. | 1 |
14.8的立方根是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | $\sqrt{2}$ |
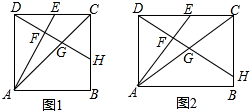
 如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.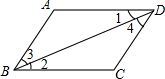 如图,下列推理是否正确,请写出你认为是正确推理的编号①②④.
如图,下列推理是否正确,请写出你认为是正确推理的编号①②④.