题目内容
8.下列各组线段中,能够组成直角三角形的一组是( )| A. | 1cm,2cm,3cm | B. | 2cm,3cm,4cm | C. | 4cm,5cm,6cm | D. | 1cm,$\sqrt{2}$cm,$\sqrt{3}$cm |
分析 先用三角形的三边的关系两边之和大于第三边,和两边之差小于第三边判断,再用勾股定理逆定理进行判断即可.
解答 解:A:12+22≠32,所以1cm,2cm,3cm不能构成三角形,即不能组成直角三角形.
B:∵2+3>4,∴2cm,3cm,4cm能构成三角形,∵22+32≠42,所以不能组成直角三角形.
C:∵4+5>6,∴4cm,5cm,6能构成三角形,∵42+52≠62,所以不能组成直角三角形,
D:∵1+$\sqrt{2}$>$\sqrt{3}$,∴1cm,$\sqrt{2}$cm,$\sqrt{3}$cm能构成三角形,∵12+($\sqrt{2}$)2=($\sqrt{3}$)2,所以能直角三角形.
故选D.
点评 此题是勾股定理逆定理题,主要考查了三角形的三边关系,勾股定理逆定理,熟练掌握勾股定理逆定理是解本题的关键.

练习册系列答案
相关题目
18.若方程组$\left\{\begin{array}{l}5x-4y=m\\ 3x+5y=8\end{array}\right.$中x与y互为相反数,则m的值是( )
| A. | 1 | B. | -1 | C. | -36 | D. | 36 |
16.下列各组二次根式中,不能合并的是( )
| A. | $\sqrt{20}$和$\sqrt{5}$ | B. | $\sqrt{12}$和$\sqrt{27}$ | C. | $\sqrt{\frac{1}{3}}$或$\sqrt{\frac{2}{3}}$ | D. | $\sqrt{45a}$和$\sqrt{125a}$ |
3. 如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
 如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )
如图,AB∥CD,∠A=60°,∠C=25°,则∠E等于( )| A. | 60° | B. | 25° | C. | 35° | D. | 45° |
13.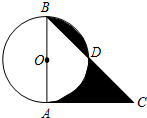 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )
 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,若∠C=45°,则图中阴影部分的面积为( )| A. | $\frac{π}{2}$ | B. | 2 | C. | π | D. | 1 |
20.举反例说明“一个锐角的余角小于这个角”是假命题,下面错误的是( )
| A. | 设一个角是45°,它的余角是45°,但45°=45° | |
| B. | 设一个角是60°,它的余角是30°,但30°<60° | |
| C. | 设一个角是30°,它的余角是60°,但60°>30° | |
| D. | 设一个角是10°,它的余角是80°,但80°>10° |
17.在直角坐标系中,点P(2x-3,x-4)在第四象限,则x的取值范围是( )
| A. | $\frac{3}{2}$<x<4 | B. | $\frac{3}{2}$≤x<4 | C. | $\frac{3}{2}$<x≤4 | D. | $\frac{3}{2}$≤x≤4 |
18. 一块直角三角板和直尺按图3方式放置,若∠1=50°,则∠2=( )度.
一块直角三角板和直尺按图3方式放置,若∠1=50°,则∠2=( )度.
 一块直角三角板和直尺按图3方式放置,若∠1=50°,则∠2=( )度.
一块直角三角板和直尺按图3方式放置,若∠1=50°,则∠2=( )度.| A. | 40° | B. | 50° | C. | 130° | D. | 140° |
 如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.
如图,正方形ABCD的边长为10,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,对角线BD相交于点H,若BD=BF,求BE的长.