题目内容
19.?ABCD中,对角线AC、BD相交于一点O,且DA=DB=2,∠DAB=60°,则△A0B的周长是( )| A. | 3cm | B. | 4cm | C. | (3+$\sqrt{3}$)cm | D. | 3$\sqrt{3}$cm |
分析 先由平行四边形的性质求出OB,再证明△ABD是等边三角形,得出AB=AD,证出四边形ABCD是菱形,得出对角线AC⊥BD,运用勾股定理求出OA,即可求出△OAB的周长.
解答 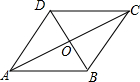 解:如图所示:
解:如图所示:
∵四边形ABCD是平行四边形,
∴OB=$\frac{1}{2}$BD=1,
∵DA=DB=2,∠DAB=60°,
∴△ABD是等边三角形,
∴AB=AD,
∴四边形ABCD是菱形,
∴AC⊥BD,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{3}$,
∴△OAB的周长=OA+OB+AB=$\sqrt{3}$+1+2=3+$\sqrt{3}$;
故选C.
点评 本题考查了平行四边形的性质、等边三角形的判定与性质、菱形的判定以及勾股定理的运用;证明四边形是菱形是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.小林在某商店购买商品A,B共三次,第一、两次均按标价购物,第三次购物时,商品A,B同时打6折,三次购物商品A,B的数量和费用如下表:
(1)求出商品A,B的标价;
(2)求第三次购物时的总费用是多少?
| 购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 |
(2)求第三次购物时的总费用是多少?
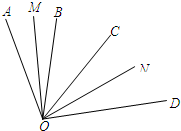 如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD. 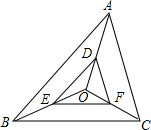 如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC.
如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC. 如图,有一块塑料矩形模板ABCD,长为10cm,宽为5cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A,D重合),在AD上适当移动三角板顶点P,能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由.
如图,有一块塑料矩形模板ABCD,长为10cm,宽为5cm,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A,D重合),在AD上适当移动三角板顶点P,能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由.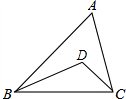 如图,在△ABC中,∠ABC和∠ACB的角平分线交于点D.
如图,在△ABC中,∠ABC和∠ACB的角平分线交于点D.