题目内容
9.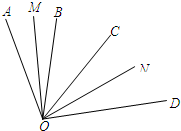 如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
如图,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD. ①若∠BOC=40°,∠MON=80°,则∠AOD的度数为120度;
②若∠AOD=x°,∠MON=80°,则∠BOC的度数为(160-x)度(用含x的代数式表示).
分析 (1)利用角平分线的定义可得∠AOM=∠BOM,∠DON=∠CON,易得∠BOM+∠CON=∠AOM+∠DON,利用∠MON-∠BOC=∠BOM+∠CON,可得结果;
(2)由角的加减可得∠AOM+∠DON,易得∠BOM+∠CON,再利用∠BOC=∠MON-(∠BOM+∠CON)可得结果.
解答 解:(1)∵∠MON-∠BOC=∠BOM+∠CON,∠BOC=40°,∠MON=80°,
∴∠BOM+∠CON=80°-40°=40°,
∵OM平分∠AOB,ON平分∠COD,
∴∠AOM=∠BOM,∠DON=∠CON,
∴∠AOM+∠DON=40°,
∴∠AOD=∠MON+∠AOM+∠DON=80°+40°=120°,
故答案为:120°;
(2)∵∠AOD=x°,∠MON=80°,
∴∠AOM+∠DON=∠AOD-∠MON=(x-80)°,
∵∠BOM+∠CON=∠AOM+∠DON=(x-80)°,
∴∠BOC=∠MON-(∠BOM+∠CON)=80°-(x-80)°=(160-x)°,
故答案为:(160-x).
点评 本题主要考查了角平分线的定义和角的加减,利用角平分线的定义得到∠BOM+∠CON=∠AOM+∠DON是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )
如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )
 如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )
如图:在△ABC中,∠ACB=90°,AC=BC,⊙O与AB相切,且点0到直线AB的距离等于△ABC中AB边上的高,与边AC,BC分别相交于点M,N,若⊙0半径为2,当⊙0在边AB上滚动时,则$\widehat{MN}$的长为( )| A. | $\frac{1}{2}$π | B. | $\frac{\sqrt{3}}{2}$π | C. | π | D. | 无法确定 |
17.下列式子正确的是( )
| A. | -3>0 | B. | -0.1>-0.01 | C. | |-2|<|-4| | D. | |-5|<4 |
14.某学校楼阶梯教室,第一排有m个座位,后面每一排都比前面一排多4个座位,则第20排座位数是( )
| A. | m+86 | B. | m+76 | C. | m+84 | D. | m+80 |
1.已知一列长a米的队伍以每分钟80米的速度向前行进,一名同学用了1分钟从队尾走到对头,那么这位同学走的路程是( )
| A. | a米 | B. | 80a米 | C. | (a+80)米 | D. | $\frac{a}{80}$米 |
19.?ABCD中,对角线AC、BD相交于一点O,且DA=DB=2,∠DAB=60°,则△A0B的周长是( )
| A. | 3cm | B. | 4cm | C. | (3+$\sqrt{3}$)cm | D. | 3$\sqrt{3}$cm |
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分图形的面积为$\frac{8π}{3}$.
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分图形的面积为$\frac{8π}{3}$.
 如图,AB∥CD,∠E=70°,则∠B+∠F+∠C=250°.
如图,AB∥CD,∠E=70°,则∠B+∠F+∠C=250°.