题目内容
7.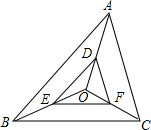 如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC.
如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC.(1)求证:△OEF∽△OBC;
(2)求证:△DEF∽△ABC.
分析 (1)根据平行线分线段成比例定理,可以得到$\frac{OE}{OB}=\frac{OF}{OC}$,利用两边成比例夹角相等即可证明.
(2)用三边成比例两个三角形相似证明即可.
解答 证明:(1)∵DE∥AB,DF∥AC,
∴$\frac{OE}{OB}=\frac{OD}{OA}$,$\frac{OF}{OC}=\frac{OD}{OA}$,
∴$\frac{OE}{OB}=\frac{OF}{OC}$,
∵∠EOF=∠BOC,
∴△OEF∽△OBC.
(2)∵DE∥AB,DF∥AC,
∴$\frac{DE}{AB}=\frac{OD}{OA}=\frac{DF}{AC}=\frac{OE}{OB}$,
∵△OEF∽△OBC,
∴$\frac{OE}{OB}=\frac{EF}{BC}$,
∴$\frac{DE}{AB}=\frac{DF}{AC}=\frac{EF}{BC}$,
∴△DEF∽△ABC.
点评 本题考查相似三角形的判定和性质、平行线的性质,灵活运用三角形相似的判定方法是解题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
17.下列式子正确的是( )
| A. | -3>0 | B. | -0.1>-0.01 | C. | |-2|<|-4| | D. | |-5|<4 |
19.?ABCD中,对角线AC、BD相交于一点O,且DA=DB=2,∠DAB=60°,则△A0B的周长是( )
| A. | 3cm | B. | 4cm | C. | (3+$\sqrt{3}$)cm | D. | 3$\sqrt{3}$cm |
 如图,AB∥CD,∠E=70°,则∠B+∠F+∠C=250°.
如图,AB∥CD,∠E=70°,则∠B+∠F+∠C=250°. 如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=8m.
如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=8m.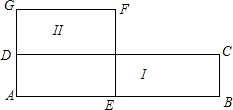 如图,一个长方形ABCD,它的长减少4cm,宽增加2cm,得到一个正方形AEFG,且正方形AEFG的面积与长方形ABCD的面积相等,求长方形ABCD的长与宽.
如图,一个长方形ABCD,它的长减少4cm,宽增加2cm,得到一个正方形AEFG,且正方形AEFG的面积与长方形ABCD的面积相等,求长方形ABCD的长与宽.