题目内容
2.【观察发现】(1)如图1,若点A、B在直线l同侧,在直线l上找一点P,使AP+BP的值最小.作法如下:作点B关于直线l的对称点B′,连接AB′,与直线l的交点就是所求的点P.(2)如图2,在等边三角形ABC中,AB=4,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
作法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为$2\sqrt{3}$.
【实践运用】
如图3,菱形ABCD中,对角线AC、BD分别为6和8,M、N分别是边BC、CD的中点,若点P是BD上的动点,则MP+PN的最小值是5.
【拓展延伸】
(1)如图4,正方形ABCD的边长为5,∠DAC的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是$\frac{5\sqrt{2}}{2}$;
(2)如图5,在四边形ABCD的对角线BD上找一点P,使∠APB=∠CPB.保留画图痕迹,并简要写出画法.

分析 【观察发现】(2)根据勾股定理求出CE的长度即为所求;
【实践运用】作点N关于BD的对称点N′,连接MN′交BD于点P,求出MN′的长度即为所求;
【拓展延伸】(1)作点D关于AE的对称点D′,过点D′作D′P⊥AD,交AE于点Q,求出D′P的长度即可;
(2)作点C关于BD的对称点C′,连接AC′并延长交于BD于点P,则点P即为所求;
解答 解:
【观察发现】(2)如图
在等边三角形ABC中,AB=4,点E是AB的中点,
∴∠BEC=90°,BE=2,BC=4,
由勾股定理可求:CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=$2\sqrt{3}$,
∴BP+PE的最小值为$2\sqrt{3}$;
【实践运用】如图3,
作点N关于BD的对称点N′,连接MN′交BD于点P,此时MP+PN的最小,MP+PN=MN′,
∵菱形ABCD中,M、N分别是边BC、CD的中点,
∴由菱形的轴对称性可知,点N′为AD的中点,
易证MN′=AB,
∵菱形ABCD中,对角线AC、BD分别为6和8,
∴∠APB=90°,AP=3,BP=4,
由勾股定理可求,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴MN′=AB=5,
∴MP+PN的最小值是5;
【拓展延伸】(1)如图4,
作点D关于AE的对称点D′,
∵AE是∠DAC的平分线,
∴点D′在AD上,
过点D′作D′P⊥AD,交AE于点Q,此时DQ+PQ最小,DQ+PQ=D′P,
∵正方形ABCD的边长为5,
∴AD′=5,∠D′AP=45°,
∴$\frac{D′P}{AD′}$=sin45°=$\frac{\sqrt{2}}{2}$,
解得;D′P=$\frac{5\sqrt{2}}{2}$,
∴DQ+PQ的最小值是$\frac{5\sqrt{2}}{2}$;
(2)
如图5,
作点C关于BD的对称点C′,连接AC′并延长交于BD于点P,则点P即为所求.
点评 此题主要考查轴对称在解决线段和最小的问题,熟悉对称点的运用和画法,知道何时线段和最小,会运用勾股定理求线段长度是解题的关键.

| A. | 4 | B. | 2 | C. | 0 | D. | 14 |
| A. | -(-$\frac{1}{2}$) | B. | |-$\frac{1}{2}$| | C. | (-$\frac{1}{2}$)0 | D. | $\sqrt{\frac{1}{2}}$ |

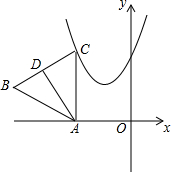 如图所示,在平面直角坐标系中,点A是x轴上一动点,过A作AC⊥x轴交抛物线y=x2+2x+2于点C,以AC为边作等边△ABC,高AD的最小值为$\frac{\sqrt{3}}{2}$.
如图所示,在平面直角坐标系中,点A是x轴上一动点,过A作AC⊥x轴交抛物线y=x2+2x+2于点C,以AC为边作等边△ABC,高AD的最小值为$\frac{\sqrt{3}}{2}$. 如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD.(1)求证:AD是⊙O的切线;
如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD.(1)求证:AD是⊙O的切线;