题目内容
14.解下列不等式组,并把它们的解集在数轴上表示出来:(1)$\left\{\begin{array}{l}{2x>3-x}\\{x+3<3x-1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x-(3x-2)≤4}\\{\frac{1-2x}{4}<1-x}\end{array}\right.$.
分析 (1)分别求出每一个不等式的解集,根据“同大取大”确定不等式组的解集,再表示在数轴上即可;
(2)分别求出每一个不等式的解集,根据“大小小大中间找”确定不等式组的解集,再表示在数轴上即可.
解答 解:(1)解不等式2x>3-x,得:x>1,
解不等式x+3<3x-1,得:x>2,
∴不等式组的解集为:x>2;
将解集表示在数轴上如图: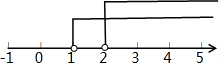
(2)解不等式x-(3x-2)≤4,得:x≥-1,
解不等式$\frac{1-2x}{4}$<1-x,得:x$<\frac{3}{2}$,
∴不等式组的解集为:-1≤x$<\frac{3}{2}$.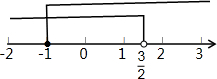
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
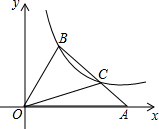 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,且tan∠BAO=$\frac{1}{2}$,OC是△OAB的中线,点B在第一象限,且其纵坐标为3,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,且tan∠BAO=$\frac{1}{2}$,OC是△OAB的中线,点B在第一象限,且其纵坐标为3,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上. 如图,D是AC上一点,DE∥AB,∠B=∠DAE,AD=AB,求证:AC=DE.
如图,D是AC上一点,DE∥AB,∠B=∠DAE,AD=AB,求证:AC=DE.