Question

12．如图，已知AB是⊙O的直径，C是⊙O上的点，且OE⊥AC于点E，过点C作⊙O的切线，交OE的延长线于点D，交AB的延长线于点F，连接AD．（1）求证：AD是⊙O的切线；
（2）若cos∠BAC=$\frac{4}{5}$，AC=8，求线段AD的长．

Answer 1

分析 （1）连接OC，由切线的性质得出∠OCD=90°，由等腰三角形的性质得出∠COD=∠AOD，由SAS证明△COD≌△AOD，得出∠OAD=∠OCD=90°，即可得出结论；
（2）由直角三角形的锐角关系证出∠ODA=∠BAC，由垂径定理得出AE=CE=$\frac{1}{2}$AC=4，由三角函数得出$\frac{DE}{AD}=\frac{4}{5}$，设DE=4x，AD=5x，则AE=3x=4，求出x，即可得出结果．

解答 （1）证明：连接OC，如图所示：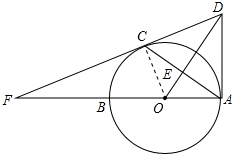
∵DC是⊙O的切线，
∴OC⊥DF，
∴∠OCD=90°，
∵OC=OA，OE⊥AC，
∴∠COD=∠AOD，
在△OAD和△OCD中，
$\left\{\begin{array}{l}{OA=OC}&{\;}\\{∠AOD=∠COD}&{\;}\\{OD=OD}&{\;}\end{array}\right.$，
∴△COD≌△AOD（SAS），
∴∠OAD=∠OCD=90°，
∴AD是⊙O的切线；
（2）解：∵∠OAD=90°，AC⊥OD，
∴∠ODA=∠BAC，AE=CE=$\frac{1}{2}$AC=4，
在Rt△ADE中，cos∠BAC=cos∠ADE=$\frac{DE}{AD}=\frac{4}{5}$，
∴设DE=4x，AD=5x，
则AE=3x=4，
∴x=$\frac{4}{3}$，
∴AD=$\frac{20}{3}$．

点评 本题考查了切线的判定与性质、全等三角形的判定与性质、垂径定理、三角函数等知识；熟练掌握切线的判定与性质，证明三角形全等是解决问题（1）的关键．