题目内容
1．解不等式组：$\left\{\begin{array}{l}{3x+6≤4x+2}\\{\frac{2x}{3}+4＜\frac{x+10}{2}}\end{array}\right.$，并把它们的解集在数轴上表示出来．分析 先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集表示在数轴上即可．
解答 解：$\left\{\begin{array}{l}{3x+6≤4x+2…①}\\{\frac{2x}{3}+4＜\frac{x+10}{2}…②}\end{array}\right.$，
解①得：x≥4，
解②得：x＜6．
则不等式组的解集是4≤x＜6．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．要注意x是否取得到，若取得到则x在该点是实心的．反之x在该点是空心的．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
11．在矩形ABCD中，AB=5，AD=12，则点A到对角线BD的距离为（ ）
| A． | $\frac{60}{13}$ | B． | 3 | C． | $\frac{5}{2}$ | D． | $\frac{13}{5}$ |
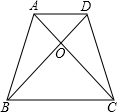如图：在梯形ABCD中两条对角线AC、BD相交于点O，已知OB=18cm，OD=12cm，则S△ABD：S△ABC=$\frac{2}{3}$．
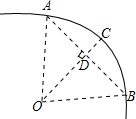如图，一条公路的转弯处是一段圆弧（图中的弧AB），点O是这段弧的圆心，C是弧AB上一点，OC⊥AB，垂足为D．若这段弯路的半径是100m，CD=20m，则A、B两点的直线距离是（ ）
如图，PA、PB分别切⊙O于A、B，∠APB=40°，则∠AOP=70°．
如图，BD平分∠ABC，DE∥AB，∠CED=80°，求∠EDB的度数．