题目内容
11. 如图,BD平分∠ABC,DE∥AB,∠CED=80°,求∠EDB的度数.
如图,BD平分∠ABC,DE∥AB,∠CED=80°,求∠EDB的度数.
分析 根据两直线平行,同位角相等,由DE∥AB得到∠ABC=∠CED=80°,再利用角平分线定义得到∠ABD=$\frac{1}{2}$∠ABC=40°,然后再利用平行线的性质可得∠EDB的度数.
解答 解:∵DE∥AB,
∴∠ABC=∠CED=80°,
∵BD平分∠ABC,
∴∠ABD=$\frac{1}{2}$∠ABC=40°,
∴∠EDB=∠ABD=40°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
6.已知三角形的两边a=3cm,b=7cm.第三边长为c,则c的长度可以是( )
| A. | 3cm | B. | 4cm | C. | 7cm | D. | 11cm |
16.若x1、x2是一元二次方程x2+ax+b=0的两个根,若x1+x2=3,则( )
| A. | a=3 | B. | a=-3 | C. | b=3 | D. | b=-3 |
1.小雨将平面直角坐标系中的三角形ABC进行平移,得到三角形A′B′C′,已知点A(2,-1)的对应点A′的坐标为(a,-4),点B(5,-2)的对应点B′的坐标为(3,b),则点C(a,b)的对应点C′的坐标为( )
| A. | (3,-4) | B. | (-2,-8) | C. | (0,-5) | D. | 无法确定 |
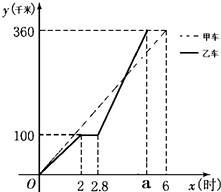 甲、乙两车同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程y(千米)与行驶时间x(时)的函数图象如图所示.
甲、乙两车同时出发从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍.两车距离A地的路程y(千米)与行驶时间x(时)的函数图象如图所示.