题目内容
11.在矩形ABCD中,AB=5,AD=12,则点A到对角线BD的距离为( )| A. | $\frac{60}{13}$ | B. | 3 | C. | $\frac{5}{2}$ | D. | $\frac{13}{5}$ |
分析 作AE⊥BD于E,由矩形的性质和勾股定理求出BD,由△ABD的面积的计算方法求出AE的长即可.
解答 解:作AE⊥BD于E,如图所示: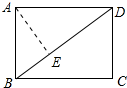
∵四边形ABCD是矩形,
∴∠BAD=90°,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∵△ABD的面积=$\frac{1}{2}$BD•AE=$\frac{1}{2}$AB•AD,
∴AE=$\frac{AB•AD}{BD}$=$\frac{5×12}{13}$=$\frac{60}{13}$;
即点A到对角线BD的距离为$\frac{60}{13}$.
故选:A.
点评 本题考查了矩形的性质、勾股定理、三角形面积的计算;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
2.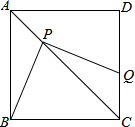 如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )
如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )
 如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )
如图,正方形ABCD,点P是对角线AC上一点,连接BP,过点P作PQ⊥BP,PQ交CD于点Q,若AP=CQ=2,则正方形ABCD的面积为( )| A. | 6+4$\sqrt{2}$ | B. | 16 | C. | 12+8$\sqrt{2}$ | D. | 32 |
16.下列计算正确的是( )
| A. | 5m-2m=3 | B. | 2a•3a=6a | C. | (ab3)2=ab6 | D. | 2m3n÷(mn)=2m2 |
3.我市5月的某一周每天的最高气温(单位:℃)统计如下:29,20,27,22,24,26,27,则这组数据的中位数与众数分别是( )
| A. | 24,27 | B. | 26,27 | C. | 26,24 | D. | 20,24 |
20.计算:$\frac{{{{(-ab)}^2}}}{{{a^2}b}}$的结果是( )
| A. | a | B. | b | C. | -b | D. | 1 |
 解不等式组,并把解集在数轴上表示出来.
解不等式组,并把解集在数轴上表示出来.