题目内容
2.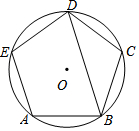 如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 144° |
分析 根据多边形内角和定理、正五边形的性质求出∠ABC、CD=CB,根据等腰三角形的性质求出∠CBD,计算即可.
解答 解:∵五边形ABCDE为正五边形,
∴∠ABC=∠C=$\frac{(5-2)×180°}{5}$=108°,
∵CD=CB,
∴∠CBD=$\frac{180°-108°}{2}$=36°,
∴∠ABD=∠ABC-∠CBD=72°,
故选B.
点评 本题考查的是正多边形和圆、多边形的内角和定理,掌握正多边形和圆的关系、多边形内角和等于(n-2)×180°是解题的关键.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
10.矩形ABCD的边AB=3 cm,AD=4 cm,以A为圆心,4 cm为半径作⊙A,则点C与⊙A的位置关系为( )
| A. | 点C在⊙A内 | B. | 点C不一定在⊙A外 | C. | 点C在⊙A上 | D. | 点C在⊙A外 |
17. 如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
 如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )| A. | BD=CD | B. | AB=AC | C. | ∠B=∠C | D. | ∠BDA=∠CDA |
14.若单项式x2ym-n与单项式-$\frac{1}{2}{x^{2m+n}}{y^3}$是同类项,那么这两个多项式的和是( )
| A. | $\frac{1}{2}{x^4}{y^6}$ | B. | $\frac{1}{2}{x^2}{y^3}$ | C. | $\frac{3}{2}{x^2}{y^3}$ | D. | $-\frac{1}{2}{x^2}{y^3}$ |
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).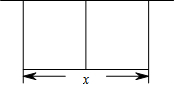 某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)
某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)