题目内容
7.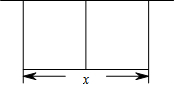 某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)
某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),己知计划中的建筑材料可建围墙的总长为50m,设两饲养室合计长x(m),总占地面积为y(m2)(1)求y关于x的函数表达式和自变量的取值范围;
(2)若要使两间饲养室占地总面积达到200m2,则各道墙的长度为多少?占地总面积有可能达到210m2吗?
分析 (1)根据题意用含x的代数式表示出饲养室的宽,由矩形的面积=长×宽计算即可;
(2)由(1)可知y是x的二次函数,根据二次函数的性质分析即可.
解答 解:(1)∵围墙的总长为50米,2间饲养室合计长x米,
∴饲养室的宽=$\frac{50-x}{3}$米,
∴总占地面积为y=x•$\frac{50-x}{3}$=-$\frac{1}{3}$x2+$\frac{50}{3}$x,(0<x<50);
(2)当两间饲养室占地总面积达到200平方米时,则-$\frac{1}{3}$x2+$\frac{50}{3}$x=200,
解得:x=20或30;
答:各道墙长分别为20米、10米或30米、10米;
当占地面积达到210平方米时,则-$\frac{1}{3}$x2+$\frac{50}{3}$x=210,
方程的△<0,所以此方程无解,
所以占地面积不可能达到210平方米;
点评 此题主要考查了由实际问题列二次函数故选以及二次函数的最值问题和一元二次方程的应用,同时也利用了矩形的性质,解题时首先正确了解题意,然后根据题意列出方程即可解决问题.

练习册系列答案
相关题目
2.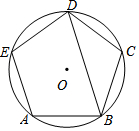 如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
 如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 144° |
 如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF.
如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF.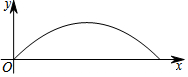 某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系
某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系 如图,己知△ABC
如图,己知△ABC