题目内容
10.矩形ABCD的边AB=3 cm,AD=4 cm,以A为圆心,4 cm为半径作⊙A,则点C与⊙A的位置关系为( )| A. | 点C在⊙A内 | B. | 点C不一定在⊙A外 | C. | 点C在⊙A上 | D. | 点C在⊙A外 |
分析 要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系;本题可由勾股定理等性质算出点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
解答 解:由勾股定理,得
AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5(cm),
∵AC>r,
点C与⊙A外边,
故选:D.
点评 本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.

练习册系列答案
相关题目
1.已知甲数比乙数的2倍少1,设甲数为x,则乙数可表示为( )
| A. | 2x-1 | B. | 2x+1 | C. | $\frac{1}{2}({x-1})$ | D. | $\frac{1}{2}({x+1})$ |
2.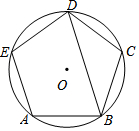 如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
 如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 144° |
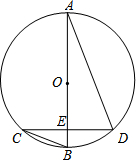 如图,AB是⊙O的直径,且点B是$\widehat{CD}$的中点,AB交CD于E,若∠C=21°,则∠ADC=69°.
如图,AB是⊙O的直径,且点B是$\widehat{CD}$的中点,AB交CD于E,若∠C=21°,则∠ADC=69°. 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置,如果BC=2,那么线段BE的长度为$\sqrt{2}$.
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿着直线AD对折,点C落在点E的位置,如果BC=2,那么线段BE的长度为$\sqrt{2}$.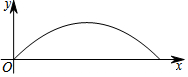 某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系
某校足球队在一次训练中,一球员从高2.4米的球门正前方m米处将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,建立如图所示的平面直角坐标系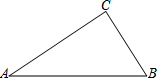 如图,己知△ABC
如图,己知△ABC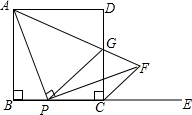 如图,在正方形ABCD中,AB=a,P为边BC上一动点(不与B、C重合),E是边BC延长线上一点,连结AP,过点P作PF⊥AP交∠DCE的平分线于点F,连结AF与边CD交于点G,连结PG.
如图,在正方形ABCD中,AB=a,P为边BC上一动点(不与B、C重合),E是边BC延长线上一点,连结AP,过点P作PF⊥AP交∠DCE的平分线于点F,连结AF与边CD交于点G,连结PG.