题目内容
12. 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2的坐标是(2,$\sqrt{3}$),点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
分析 由等边三角形的性质即可得出点B1、B2、B3、…,的坐标,根据坐标的变化即可得出变化规律“点Bn的坐标为($\frac{n}{2}$,$\frac{n\sqrt{3}}{2}$)(n为自然数)”,进而即可得出“点An的坐标为($\frac{n}{2}$+1,$\frac{n\sqrt{3}}{2}$)(n为自然数)”,依此规律即可得出结论.
解答 解:∵△OAB1,△B1A1B2,△B2A2B3,…,都是边长为1的等边三角形,
∴B1A1∥x轴,B2A2∥x轴,…,BnAn∥x轴,
∴点B1的坐标为($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点B2的坐标为(1,$\sqrt{3}$),
点B3的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$),点B4的坐标为(2,2$\sqrt{3}$),…,
∴点Bn的坐标为($\frac{n}{2}$,$\frac{n\sqrt{3}}{2}$)(n为自然数),
∴点An的坐标为($\frac{n}{2}$+1,$\frac{n\sqrt{3}}{2}$)(n为自然数).
当n=2时,点A2的坐标为(2,$\sqrt{3}$);
当n=2017时,点A2017的坐标为($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
点评 本题考查了规律型中点的坐标,根据等边三角形的性质结合点的变化找出变化规律“点An的坐标为($\frac{n}{2}$+1,$\frac{n\sqrt{3}}{2}$)(n为自然数)”是解题的关键.

练习册系列答案
相关题目
1.已知甲数比乙数的2倍少1,设甲数为x,则乙数可表示为( )
| A. | 2x-1 | B. | 2x+1 | C. | $\frac{1}{2}({x-1})$ | D. | $\frac{1}{2}({x+1})$ |
2.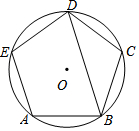 如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
 如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )
如图,正五边形ABCDE内接于⊙O,则∠ABD的度数为( )| A. | 36° | B. | 72° | C. | 108° | D. | 144° |
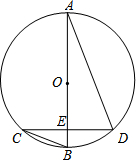 如图,AB是⊙O的直径,且点B是$\widehat{CD}$的中点,AB交CD于E,若∠C=21°,则∠ADC=69°.
如图,AB是⊙O的直径,且点B是$\widehat{CD}$的中点,AB交CD于E,若∠C=21°,则∠ADC=69°.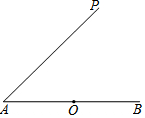 如图,已知O是∠PAB的一边AB上的点,按要求作图:
如图,已知O是∠PAB的一边AB上的点,按要求作图: 如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF.
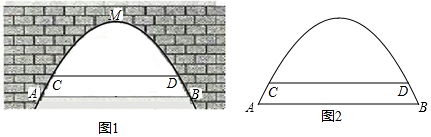
如图,若AB是CD的垂直平分线,E,F是AC,AD的中点,连结BE,BF. 如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成,若墙长为18米,设这个苗圃垂直于墙的一边长为x米.
如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成,若墙长为18米,设这个苗圃垂直于墙的一边长为x米.