题目内容
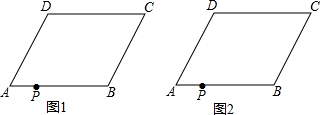
16.如图,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上.(1)判断四边形ABCD的形状并加以证明;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.
①在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由);
②如果∠C=60°,那么$\frac{AP}{PB}$为何值时,B′P⊥AB.
分析 (1)根据两组对边分别平行的四边形是平行四边形进行判断;
(2)①根据轴对称的性质进行作图即可;②先根据折叠得出一些对应边相等,对应角相等,并推导出B′D=B′E,再设AP=a,BP=b,利用解直角三角形将DQ和CQ长用含a的代数式表示出来,最后根据CD=DQ+CQ列出关于a、b的关系式,求得a、b的比值即可.
解答 解:(1)四边形ABCD是平行四边形
证明:∵在四边形ABCD中,AD∥BC,
∴∠A+∠B=180°,
∵∠A=∠C,
∴∠C+∠B=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形;
(2)①四边形PB′C′Q如下:
②当AB=AD时,平行四边形ABCD是菱形,
由折叠可得,BP=B′P,CQ=C′Q,BC=B′C′,∠C=∠C′=60°=∠A,
当B′P⊥AB时,由B′P∥C′Q,可得C′Q⊥CD,
设AD与B'P交于点E,
∴∠PEA=30°=∠DEB′,∠QDC′=30°=∠B′DE,
∴B′D=B′E,
设AP=a,BP=b,则直角三角形APE中,PE=$\sqrt{3}$a,且B′P=b,BC=B′C′=CD=a+b,
∴B′E=b-$\sqrt{3}$a=B′D,
∴C′D=a+b-(b-$\sqrt{3}$a)=a+$\sqrt{3}$a,
∴直角三角形C′QD中,C′Q=$\frac{1+\sqrt{3}}{2}$a=CQ,DQ=$\sqrt{3}$C′Q=$\frac{\sqrt{3}+3}{2}$a,
∵CD=DQ+CQ=a+b,
∴$\frac{\sqrt{3}+3}{2}$a+$\frac{1+\sqrt{3}}{2}$a=a+b,
整理得($\sqrt{3}$+1)a=b,
∴$\frac{a}{b}$=$\frac{1}{\sqrt{3}+1}$=$\frac{\sqrt{3}-1}{2}$,即$\frac{AP}{PB}$=$\frac{\sqrt{3}-1}{2}$.
点评 本题主要考查了平行四边形以及菱形,解题的关键是掌握平行四边形的判定以及菱形的判定与性质.在解题时注意,菱形的四条边都相等,此外在折叠问题中,需要抓住对应边相等,对应角相等这些等量关系,折叠问题的实质是轴对称的性质.

| A. | 菱形的对角线互相平分 | B. | 正方形的对角线互相垂直平分 | ||
| C. | 矩形的对角线相等且平分 | D. | 平行四边形的对角线相等且垂直 |
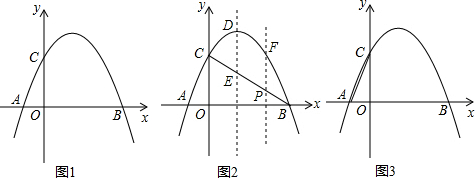
 如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
 如图,用一个半径为30cm,面积为450πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
如图,用一个半径为30cm,面积为450πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )| A. | 5cm | B. | 10cm | C. | 15cm | D. | 5πcm |
| A. | -5 | B. | 0 | C. | $\sqrt{8}$ | D. | 3 |
 如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )
如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )| A. | 40海里 | B. | 40$\sqrt{2}$海里 | C. | 40$\sqrt{3}$海里 | D. | 40$\sqrt{6}$海里 |
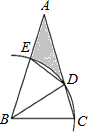 如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )
如图,△ABC中,∠A=30°,AB=AC,BC=2,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E,则线段AE、AD与$\widehat{DE}$围成的阴影部分的面积是 ( )| A. | 2$\sqrt{3}$+2-$\frac{5}{6}$π | B. | $\sqrt{3}$+1-$\frac{5}{3}$π | C. | 2$\sqrt{3}$+2-$\frac{1}{2}$π | D. | $\sqrt{3}$+1-$\frac{1}{2}$π |