题目内容
11. 如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①2a+b=0;②当-1≤x≤3时,y≤0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 根据抛物线对称轴可判断①;根据图象知当-1≤x≤3时图象位于x轴下方或在x轴上,可判断②;根据函数对称轴即可判断增减性,可判断③;由图象过(3,0)可判断④.
解答 解:由图象可知,当x=-1时,y=0;当x=3时,y=0;
∴抛物线的对称轴为x=$\frac{-1+3}{2}$=1,即-$\frac{b}{2a}$=1,得:2a+b=0,故①正确;
由图象可知,当-1≤x≤3时,y≤0,故②正确;
由图象可知,当x1<x2<1时,y1>y2,故③错误;
∵抛物线过(3,0),
∴当x=3时,y=0,即9a+3b+c=0,故④正确;
故答案为:①②④.
点评 本题考查了二次函数图象与系数的关系,解题的关键是结合图象逐条分析.解决该题型题目时,结合图象上的点找出二次函数各系数间的关系是关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
2.$\sqrt{81}$的平方根是( )
| A. | 81 | B. | ±3 | C. | -3 | D. | 3 |
19.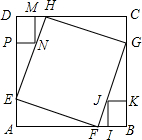 正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
 正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )| A. | 10 | B. | 3$\sqrt{10}$ | C. | 4$\sqrt{5}$ | D. | 3$\sqrt{10}$或4$\sqrt{5}$ |
6.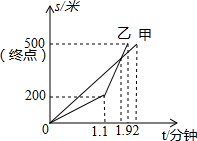 在2015年聊城市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )
在2015年聊城市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )
 在2015年聊城市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )
在2015年聊城市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,其中错误的是( )| A. | 这次比赛的全程是500米 | |
| B. | 乙队先到达终点 | |
| C. | 比赛中两队从出发到1.1分钟时间段,乙队的速度比甲队的速度快 | |
| D. | 乙与甲相遇时乙的速度是375米/分钟 |
3.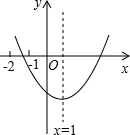 如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①b2>4ac,②2a+b=0,③3a+c>0,④4a-2b+c<0;⑤9a+3b+c<0.其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①b2>4ac,②2a+b=0,③3a+c>0,④4a-2b+c<0;⑤9a+3b+c<0.其中正确的是( )
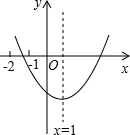 如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①b2>4ac,②2a+b=0,③3a+c>0,④4a-2b+c<0;⑤9a+3b+c<0.其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象,有下列判断:①b2>4ac,②2a+b=0,③3a+c>0,④4a-2b+c<0;⑤9a+3b+c<0.其中正确的是( )| A. | ①②③ | B. | ②③④ | C. | ①②⑤ | D. | ③④⑤ |
20.下列运算正确的是( )
| A. | ($\frac{1}{2}$)-1=-$\frac{1}{2}$ | B. | 5÷(-2)×$\frac{1}{2}$=5÷(-1)=-5 | ||
| C. | (2a+b)2=4a2+4ab+b2 | D. | a2•(ab)3=a4b2 |
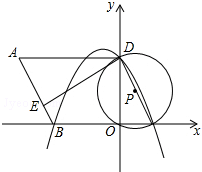 如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.
如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.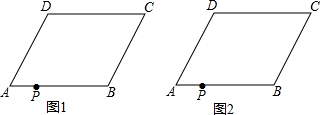
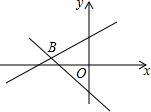 一次函数y=ax+3,与y=bx-1的图象如图所示,其交点B(-3,m),则不等式ax+3>bx-1的解集表示在数轴上正确的是( )
一次函数y=ax+3,与y=bx-1的图象如图所示,其交点B(-3,m),则不等式ax+3>bx-1的解集表示在数轴上正确的是( )


