题目内容
5. 如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )
如图,岛P位于岛Q的正西方,P、Q两岛间的距离为20(1+$\sqrt{3}$)海里,由岛P、Q分别测得船R位于南偏东60°和南偏西45°方向上,则船R到岛P的距离为( )| A. | 40海里 | B. | 40$\sqrt{2}$海里 | C. | 40$\sqrt{3}$海里 | D. | 40$\sqrt{6}$海里 |
分析 要求PR的长,需要构造直角三角形,作辅助线RA⊥PQ,然后根据题目中的条件可以得到PR的长,本题得以解决.
解答  解:作RA⊥PQ于点A,如右图所示,
解:作RA⊥PQ于点A,如右图所示,
∵∠QPR=30°,∠PQR=45°,∠PAR=∠QAR=90°,PQ=20(1+$\sqrt{3}$)海里,
∴PA=$\frac{RA}{tan30°}$,QA=$\frac{RA}{tan45°}$,PR=2RA,
∴$\frac{RA}{\frac{\sqrt{3}}{3}}+\frac{RA}{1}$=20(1+$\sqrt{3}$),
解得,RA=20海里,
∴PR=2RA=40海里,
故选A.
点评 本题考查解直角三角形的应用-方向角问题,解题的关键是明确题意,作出合适的辅助线,利用特殊角的三角函数值进行解答.

练习册系列答案
相关题目
15.关于二次函数y=x2-2x+1-a2图象,以下判断错误的是( )
| A. | 开口方向确定 | B. | 对称轴位置确定 | ||
| C. | 与y轴的交点一定在正半轴 | D. | 与x轴的交点一定有一个在正半轴 |
13.化简($\frac{x}{x-1}$-$\frac{2x+2}{{x}^{2}-1}$)$÷\frac{x-2}{{x}^{2}-x}$的结果是( )
| A. | x | B. | $\frac{1}{x}$ | C. | $\frac{x+1}{x-1}$ | D. | $\frac{x-1}{x+1}$ |
20.下列运算正确的是( )
| A. | ($\frac{1}{2}$)-1=-$\frac{1}{2}$ | B. | 5÷(-2)×$\frac{1}{2}$=5÷(-1)=-5 | ||
| C. | (2a+b)2=4a2+4ab+b2 | D. | a2•(ab)3=a4b2 |
10. 已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )
已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )
 已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )
已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
14.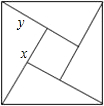 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
15. 一个几何体的三视图如图所示,那么这个几何体的形状是( )
一个几何体的三视图如图所示,那么这个几何体的形状是( )
 一个几何体的三视图如图所示,那么这个几何体的形状是( )
一个几何体的三视图如图所示,那么这个几何体的形状是( )| A. |  | B. |  | C. |  | D. |  |
 已知反比例函数的两支图象关于原点对称,利用这一结论解决下列问题:如图,在同一直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D,已知点A(-m,O)、C(m,0).
已知反比例函数的两支图象关于原点对称,利用这一结论解决下列问题:如图,在同一直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{\sqrt{3}}{x}$的图象分别交于第一、三象限的点B,D,已知点A(-m,O)、C(m,0).