题目内容
1. 如图,用一个半径为30cm,面积为450πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )
如图,用一个半径为30cm,面积为450πcm2的扇形铁皮,制作一个无底的圆锥(不计损耗),则圆锥的底面半径r为( )| A. | 5cm | B. | 10cm | C. | 15cm | D. | 5πcm |
分析 利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得到$\frac{1}{2}$•2πr•30=450π,然后解方程即可.
解答 解:根据题意得$\frac{1}{2}$•2πr•30=450π,解得r=15,
即圆锥的底面半径r为15cm.
故选C.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.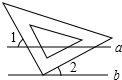 如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
 如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )| A. | 45° | B. | 36° | C. | 54° | D. | 126° |
13.化简($\frac{x}{x-1}$-$\frac{2x+2}{{x}^{2}-1}$)$÷\frac{x-2}{{x}^{2}-x}$的结果是( )
| A. | x | B. | $\frac{1}{x}$ | C. | $\frac{x+1}{x-1}$ | D. | $\frac{x-1}{x+1}$ |
10. 已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )
已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )
 已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )
已知,△ABC中,AB=AC,BE∥AC,∠BDE=110°,∠BAD=70°,则∠E=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
11.借助计算器可求得$\sqrt{{4^2}+{3^2}}=5,\sqrt{{{44}^2}+{{33}^2}}=55,\sqrt{{{444}^2}+{{333}^2}}$=555,…,仔细观察上面几道题的计算结果,试猜想$\sqrt{{{\underbrace{44…4}_{2016个}}^2}+{{\underbrace{33…3}_{2016个}}^2}}$=( )
| A. | $\underbrace{55…5}_{2013个}$ | B. | $\underbrace{55…5}_{2014个}$ | C. | $\underbrace{55…5}_{2015个}$ | D. | $\underbrace{55…5}_{2016个}$ |
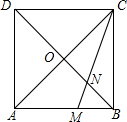 如图,正方形ABCD的边长为3,对角线AC与BD相交于点O,CM交BD于点N,若BM=1,则线段ON的长为$\frac{3\sqrt{2}}{4}$.
如图,正方形ABCD的边长为3,对角线AC与BD相交于点O,CM交BD于点N,若BM=1,则线段ON的长为$\frac{3\sqrt{2}}{4}$.
 如图是由四个小正方体搭成的一个几何体,这个几何体的俯视图是( )
如图是由四个小正方体搭成的一个几何体,这个几何体的俯视图是( )


