题目内容
4.在一个暗盒中放有若干个白色球和2个黑色球(这些球除颜色外无其他区别),若从中随机取出1个球是白色的概率是0.6,那么在暗盒中随机取出2个球恰好都是白色球的概率是0.3.分析 首先设有x个白球,由概率公式可得:$\frac{x}{x+2}$=0.6,解此方程即可求得白球的个数,再根据题意画出树状图,由树状图求得所有等可能的结果与在暗盒中随机取出2个球恰好都是白色球的情况,继而求得答案.
解答 解:设有x个白球,
根据题意得:$\frac{x}{x+2}$=0.6,
解得:x=3,
经检验:x=3是原分式方程的解;
画树状图得: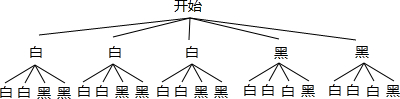
∵共有20种等可能的结果,在暗盒中随机取出2个球恰好都是白色球的有6种情况,
∴在暗盒中随机取出2个球恰好都是白色球的概率是:$\frac{6}{20}$=0.3.
故答案为:0.3.
点评 此题考查了列表法或树状图法求概率.注意利用方程思想求得白球的个数是关键.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
15.关于二次函数y=x2-2x+1-a2图象,以下判断错误的是( )
| A. | 开口方向确定 | B. | 对称轴位置确定 | ||
| C. | 与y轴的交点一定在正半轴 | D. | 与x轴的交点一定有一个在正半轴 |
19.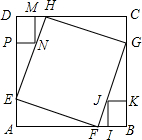 正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
 正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )
正方形ABCD的边长为12,在其角上去掉两个全等的矩形DMNP和矩形BIJK,DM=IB=2,DP=BK=3,正方形EFGH顶点分别在正方形ABCD的边上,且EH过N点,则正方形EFGH的边长是( )| A. | 10 | B. | 3$\sqrt{10}$ | C. | 4$\sqrt{5}$ | D. | 3$\sqrt{10}$或4$\sqrt{5}$ |
9.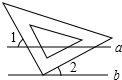 如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
 如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )| A. | 45° | B. | 36° | C. | 54° | D. | 126° |
13.化简($\frac{x}{x-1}$-$\frac{2x+2}{{x}^{2}-1}$)$÷\frac{x-2}{{x}^{2}-x}$的结果是( )
| A. | x | B. | $\frac{1}{x}$ | C. | $\frac{x+1}{x-1}$ | D. | $\frac{x-1}{x+1}$ |
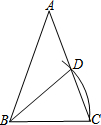 如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,交AC于点D,连接BD,则∠ABD=36°.
如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,交AC于点D,连接BD,则∠ABD=36°.
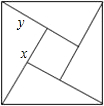 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x-y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )