Question

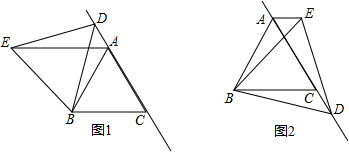
1．感知：如图①，正方形AEFG的顶点E，F在正方形ABCD的内部，连接BE，DG，可知△ABE≌△ADG．（不需证明）
探究：如图②，菱形AEFG的顶点E在菱形ABCD的内部，∠BAD=∠EAG，连接BE，DG，求证：△ABE≌△ADG．
应用：如图③，△ADE的顶点D在△ABC的内部，∠BAC=∠DAE=120°，AB=AC=6，AD=AE，求阴影部分图形的面积．

Answer 1

分析 （1）根据正方形的性质得出AD=AB，AG=AE，∠BAD=∠EAG=90°，进而得出∠BAE=∠DAG，然后根据SAS即可证得△ABE≌△ADG．
（2）根据菱形的性质得出AD=AB，AG=AE，进而得出∠BAE=∠DAG，然后根据SAS即可证得△ABE≌△ADG．
（3）过点A作AM⊥BC于M，根据等腰三角形的性质得出BC=2CM，∠ACB=∠ABC=30°，进而求得AM=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3，CM=$\sqrt{A{C}^{2}-A{M}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$，BC=2×3$\sqrt{3}$=6$\sqrt{3}$，然后根据SAS证得△ABD≌△ACE，从而得出阴影部分图形面积即为△ABC的面积，求得△ABC的面积即可．

解答 解：感知：∵四边形AEFG和四边形ABCD是正方形，
∴AD=AB，AG=AE，∠BAD=∠EAG=90°，
∴∠BAD-∠EAD=∠EAG-∠EAD，
即∠BAE=∠DAG，
在△ABE和△ADG中，
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAG}\\{AE=AG}\end{array}\right.$
∴△ABE≌△ADG（SAS）；
探究：∵∠BAD=∠EAG，
∴∠BAD-∠EAD=∠EAG-∠EAD，
即∠BAE=∠DAG，
∵四边形AEFG和四边形ABCD是菱形，
∴AB=AD，AE=AG，
在△ABE和△ADG中，
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAG}\\{AE=AG}\end{array}\right.$
∴△ABE≌△ADG（SAS）；
应用：过点A作AM⊥BC于M，
∵AB=AC=6，∠BAC=120°，
∴BC=2CM，∠ACB=∠ABC=30°，
在RT△ACM中，AM=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3，
CM=$\sqrt{A{C}^{2}-A{M}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$，
∴BC=2×3$\sqrt{3}$=6$\sqrt{3}$，
∵∠BAC=∠DAE=120°，
∴∠BAC-∠CAD=∠DAE-∠CAD，
即∠BAD=∠CAE，
在△ABD和△ACE中，
$\left\{\begin{array}{l}{AD=AE}\\{∠BAD=∠CAE}\\{AB=AC}\end{array}\right.$
∴△ABD≌△ACE（SAS）；
∴阴影部分图形面积即为△ABC的面积，
∴阴影部分图形面积为：$\frac{1}{2}$BC•AM=$\frac{1}{2}$×6$\sqrt{3}$×3=9$\sqrt{3}$．

点评 本题是四边形的综合题，考查了三角形全等的判定和性质，正方形的性质，菱形的性质，解直角三角形和勾股定理的应用等，熟练掌握性质定理是解题的关键．